The resistance Rt of a conductor varies with temperature t as shown in the figure. If the variation is represented by , then

(1) α and β are both negative
(2) α and β are both positive
(3) α is positive and β is negative
(4) α is negative and β are positive

Variation of current and voltage in a conductor has been shown in the diagram below. The resistance of the conductor is :
(1) 4 ohm
(2) 2 ohm
(3) 3 ohm
(4) 1 ohm
Resistance as shown in figure is negative at
(1) A
(2) B
(3) C
(4) None of these
For a cell, the graph between the potential difference \((V)\) across the terminals of the cell and the current \((I)\) drawn from the cell is shown in the figure below. The emf and the internal resistance of the cell are, respectively:

| 1. | \(2~\text{V}, 0.5 ~\Omega\) | 2. | \(2~\text{V}, 0.4 ~\Omega\) |
| 3. | \(>2~\text{V}, 0.5 ~\Omega\) | 4. | \(>2~\text{V}, 0.4 ~\Omega\) |
The graph which represents the relation between the total resistance R of a multi-range moving coil voltmeter and its full-scale deflection V is :
1. (i)
2. (ii)
3. (iii)
4. (iv)
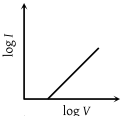
When a current I is passed through a wire of constant resistance, it produces a potential difference V across its ends. The graph drawn between log I and log V will be
(1)
(2)
(3)
(4)
The V-I graph for a conductor at temperature T1 and T2 are as shown in the figure. is proportional to :
(1)
(2)
(3)
(4)
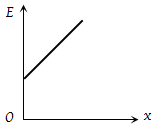
A cylindrical conductor has a uniform cross-section. The resistivity of its material increases linearly from the left end to the right end. If a constant current is flowing through it and at a section distance x from the left end, the magnitude of electric field intensity is E, which of the following graphs is correct :
(1)
(2)
(3)
(4)
The V-I graph for a conductor makes an angle θ with V-axis. Here V denotes the voltage and I denotes current. The resistance of the conductor is given by :
(1)
(2)
(3)
(4)
A battery consists of a variable number \('n'\) of identical cells having internal resistances connected in series. The terminals of battery are short circuited and the current \(i\) is measured. The graph below that shows the relationship between \(i\) and \(n\) is:
| 1. |  |
2. |  |
| 3. |  |
4. |  |