A particle is subjected to two simple harmonic motions in the same direction having equal amplitudes and equal frequency. If the resulting amplitude is equal to the amplitude of individual motions, the phase difference between them will be:

1.  $\frac{\mathrm{\pi }}{3}$

2.  $\frac{2\mathrm{\pi }}{3}$

3.  $\frac{\mathrm{\pi }}{6}$

4.  $\frac{\mathrm{\pi }}{2}$

The motion of a particle varies with time according to the relation $\mathrm{y}$ $=\mathrm{a}$ $\sin$ $\mathrm{\omega t}+\mathrm{a}$ $\cos$ $\mathrm{\omega t}$. Then:

If a particle is executing SHM, with an amplitude A, the distance moved and the displacement of the body in a time equal to its time period are, respectively:

The equations of the displacement of two particles making SHM are represented by y₁ = a sin (ωt + φ) and y₂ = a cos (ωt) respectively. The phase difference of the velocities of the two particles will be:
1. π/2 + φ
2. -φ
3. φ
4. φ - π/2

 The displacement of a particle executing SHM is given by y = 0.25 (sin 200t) cm. The maximum speed of the particles is:

1.  200 cm/sec

2.  100 cm/sec

3.  50 cm/sec

4.  0.25 cm/sec

Which of the following figure represents damped harmonic motion?

(i)
(ii)
(iii)
(iv)

1. (i) and (ii)

2. (iii) and (iv)

3. (i), (ii), (iii), and (iv)

4. (i) and  (iv)

A particle is executing SHM with an amplitude \(A\) and the time period \(T\). If at \(t=0\), the particle is at its origin (mean position), then the time instant when it covers a distance equal to \(2.5A\) will be:
1. \( \frac{T}{12} \)
2. \(\frac{5 T}{12} \)
3. \( \frac{7 T}{12} \)
4. \( \frac{2 T}{3}\)

The time period of a spring mass system at the surface of earth is 2 second. What will be the time period of this system on the moon where acceleration due to gravity is $\frac{1}{6}\mathrm{th}$ of the value of g on earth's surface?

A particle undergoes SHM with a time period of 2 seconds. In how much time will it travel from its mean position to a displacement equal to half of its amplitude?

(1) $\frac{1}{2}s$

(2) $\frac{1}{6}s$

(3) $\frac{1}{4}s$

(4) $\frac{1}{3}s$

The uniform stick of mass m length L is pivoted at the centre. In the equilibrium position shown in the figure, the identical light springs have their natural length. If the stick is turned through a small angle $\theta$, it executes SHM. The frequency of the motion is:

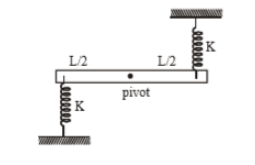
(1) $\frac{1}{2\mathrm{\pi }}\sqrt{\frac{6K}{m}}$

(2) $\frac{1}{2\mathrm{\pi }}\sqrt{\frac{3K}{2m}}$

(3) $\frac{1}{2\mathrm{\pi }}\sqrt{\frac{3K}{m}}$

(4) None of these