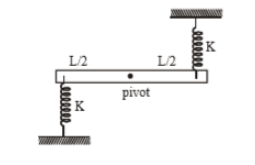
The uniform stick of mass m length L is pivoted at the centre. In the equilibrium position shown in the figure, the identical light springs have their natural length. If the stick is turned through a small angle , it executes SHM. The frequency of the motion is:
(1)
(2)
(3)
(4) None of these

If the displacement x and the velocity v of a particle executing simple harmonic motion are related through the expression ,then its time period will be:
| 1. | \(\pi \) | 2. | \(2 \pi \) |
| 3. | \(4 \pi \) | 4. | \(6 \pi\) |
A simple pendulum is oscillating without damping. When the displacement of the bob is less than maximum, its acceleration vector is correctly shown in:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
A particle undergoes SHM with a time period of 2 seconds. In how much time will it travel from its mean position to a displacement equal to half of its amplitude?
(1)
(2)
(3)
(4)
A second's pendulum is mounted in a rocket. Its period of oscillation decreases when the rocket:
(1) Comes down with uniform acceleration
(2) Moves around the earth in a geostationary orbit
(3) Moves up with a uniform velocity
(4) Moves up with the uniform acceleration
There is a simple pendulum hanging from the ceiling of a lift. When the lift is stand still, the time period of the pendulum is T. If the resultant acceleration becomes g/4, then the new time period of the pendulum is
(1) 0.8 T
(2) 0.25 T
(3) 2 T
(4) 4 T
The time period of a spring mass system at the surface of earth is 2 second. What will be the time period of this system on the moon where acceleration due to gravity is of the value of g on earth's surface?
| 1. | \(\frac{1}{\sqrt{6}} ~\mathrm{seconds} \) | 2. | \(2 \sqrt{6}~ \mathrm{seconds} \) |
| 3. | \(2~ \mathrm{seconds} \) | 4. | \( 12~\mathrm{ seconds}\) |
A particle is executing SHM with an amplitude \(A\) and the time period \(T\). If at \(t=0\), the particle is at its origin (mean position), then the time instant when it covers a distance equal to \(2.5A\) will be:
1. \(
\frac{T}{12}
\)
2. \(\frac{5 T}{12}
\)
3. \( \frac{7 T}{12}
\)
4. \( \frac{2 T}{3}\)
A block P of mass m is placed on a frictionless horizontal surface. Another block Q of same mass is kept on P and connected to the wall with the help of a spring of spring constant k as shown in the figure. μs is the coefficient of friction between P and Q. The blocks move together performing SHM of amplitude A. The maximum value of the friction force between P and Q will be:

1. kA
2.
3. Zero
4. μs mg
Which of the following figure represents damped harmonic motion?
| (i) |  |
| (ii) |  |
| (iii) |  |
| (iv) |  |
1. (i) and (ii)
2. (iii) and (iv)
3. (i), (ii), (iii), and (iv)
4. (i) and (iv)
