A simple pendulum is set up in a trolley which moves to the right with an acceleration a on a horizontal plane. Then the thread of the pendulum in the mean position makes an angle with the vertical
1. in the forward direction
2. in the upward direction
3. in the backward direction
4. in the forward directions
A pendulum bob is suspended in a Car moving horizontally with acceleration ‘a’ the angle the string will make with vertical is
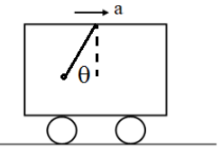
1.
2.
3.
4.
In the arrangement shown, the ends \(P\) and \(Q\) of an inextensible string move downwards with uniform speed \(v.\) The pulleys \(A\) and \(B\) are fixed. The mass \(M\) moves upward with a speed of:
1. \(2 v \cos \theta\)
2. \(v \cos \theta\)
3. \(\left(\frac{2 v}{\cos \theta}\right)\)
4. \(\left(\frac{v}{\cos \theta}\right)\)
A block of mass is placed on the floor of lift which is moving with velocity = , where is time in second and velocity m/s. Find the time at which normal force on the block is three times of its weight.
1. (3g/8)s
2. g s
3. g/4 s
4. 3g s
Two blocks of masses 2 and are connected as shown in the figure. Now the string between the blocks is suddenly cut. Then, at that instant, accelerations of the blocks A and B will be
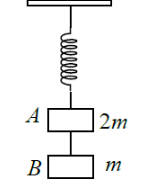
1. g and g, respectively
2. g and g/2, respectively
3. g/2 and g, respectively
4. g/2 and g/2, respectively
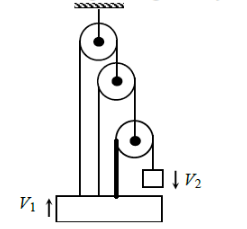
1. \(7v_1-v_2=0\)
2. \(7v_1+v_2=0\)
3. \(v_1+v_2=0\)
4. \(v_1+3v_2=0\)
Using constraint equations relation between and will be
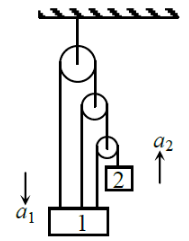
1. =3
2. a =3
3. a= 6
4. a= 7
A block of mass 2 kg is hanging with two identical massless springs as shown in figure. The acceleration of the block just at the moment, the right spring breaks is (g = 10 )
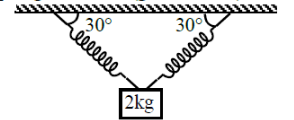
1. 10
2. 25
3. 5
4. 4
A piece of wire is bent in the shape of a parabola y = (y-axis vertical) with a
bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is
1.
2.
3.
4.
Three block of masses m, M and M’ are arranged as shown in fig. The surfaces are frictionless, pulley and strings are ideal. The mass M’ of the hanging block which will prevent the smaller block (m) from slipping over the wedge will be
1.
2.
3.
4.



