Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time . On other days, if she remains stationary on the moving escalator, then the escalator takes her up in time . The time taken by her to walk up on the moving escalator will be
1.
2.
3.
4.
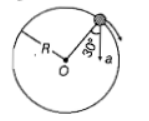
In the given figure, represents the total acceleration of a particle moving in the clockwise direction in a circle of radius R=2.5 m at a given instant of time. The speed of the particle is:
1. 4.5 m/s
2. 5.0 m/s
3. 5.7 m/s
4. 6.2 m/s
A particle moves so that its position vector is given by \(r=\cos \omega t \hat{x}+\sin \omega t \hat{y}\) where \(\omega\) is a constant. Based on the information given, which of the following is true?
| 1. | The velocity and acceleration, both are parallel to \(r.\) |
| 2. | The velocity is perpendicular to \(r\) and acceleration is directed towards the origin. |
| 3. | The velocity is not perpendicular to \(r\) and acceleration is directed away from the origin. |
| 4. | The velocity and acceleration, both are perpendicular to \(r.\) |
A particle of mass 10g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration, if the kinetic energy of the particle becomes equal to 8x10-4 J by the end of the second revolution after the beginning of the motion?
1. 0.15 m/s2
2. 0.18 m/s2
3. 0.2 m/s2
4. 0.1 m/s2
A ship A is moving Westwards with a speed of 10 km h-1 and a ship B 100 km South of A, is moving Northwards with a speed of 10 km h-1. The time after which the distance between them becomes shortest is
1., h
2. 5h
3. 5h
4. 10h
A projectile is fired from the surface of the earth with a velocity of 5 m/s and angle with the horizontal. Another projectile fired from another planet with a velocity of 3 m/s at the same angle follows a trajectory, which is identical to the trajectory of the projectile fired from the earth. The value of the acceleration due to gravity on the planet (in m/s2) is: [Given, g = 9.8 m/s2]
1. 3.5
2. 5.9
3. 16.3
4. 110.8
A particle is moving such that its position coordinates (x, y) are (2m, 3m) at time t = 0, (6m, 7m) at time t = 2s and (13m, 14m) at time t = 5s. Average velocity vector (vav) from t = 0 to t = 5s is
1. (13+14)
2. (+)
3. 2(+)
4. (+)
The velocity of a projectile at the initial point A is (2i + 3j) m/s. Its velocity (in m/s) at point B is:
1. -2i+3j
2. -2i-3j
3. 2i-3j
4. 2i+3j
The horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is:
1.
2.
3.
4.
A particle has an initial velocity (\(2\hat{i}+3\hat{j}\)) and an acceleration (\(0.3\hat{i}+0.2\hat{j}\)). The magnitude of velocity after \(10\) s will be:
1. \(9 \sqrt{2} ~\text{units} \)
2. \(5 \sqrt{2} ~\text{units} \)
3. \(5 ~\text{units} \)
4. \(9~\text{units} \)