The voltage V and current I graph for a conductor at two different temperatures T1 and T2 are shown in the figure. The relation between T1 and T2 is :
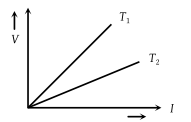
(1) T1 > T2
(2)
(3) T1 = T2
(4) T1 < T2

From the graph between current \(I\) and voltage \(V\) shown below, identify the portion corresponding to negative resistance
1. \(AB\)
2. \(BC\)
3. \(CD\)
4. \(DE\)
I-V characteristic of a copper wire of length L and area of cross-section A is shown in figure. The slope of the curve becomes :
(1) More if the experiment is performed at higher temperature
(2) More if a wire of steel of same dimension is used
(3) More if the length of the wire is increased
(4) Less if the length of the wire is increased
E denotes electric field in a uniform conductor, I corresponding current through it, Vd drifts velocity of electrons and P denotes thermal power produced in the conductor, then which of the following graph is incorrect :
(1)
(2)
(3)
(4)
The two ends of a uniform conductor are joined to a cell of e.m.f. E and some internal resistance. Starting from the midpoint P of the conductor, we move in the direction of current and return to P. The potential V at every point on the path is plotted against the distance covered (x). Which of the following graphs best represents the resulting curve
(1)
(2)
(3)
(4)
The resistance Rt of a conductor varies with temperature t as shown in the figure. If the variation is represented by , then
(1) α and β are both negative
(2) α and β are both positive
(3) α is positive and β is negative
(4) α is negative and β are positive
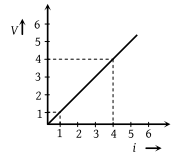
Variation of current and voltage in a conductor has been shown in the diagram below. The resistance of the conductor is :
(1) 4 ohm
(2) 2 ohm
(3) 3 ohm
(4) 1 ohm
Resistance as shown in figure is negative at
(1) A
(2) B
(3) C
(4) None of these
For a cell, the graph between the potential difference \((V)\) across the terminals of the cell and the current \((I)\) drawn from the cell is shown in the figure below. The emf and the internal resistance of the cell are, respectively:

| 1. | \(2~\text{V}, 0.5 ~\Omega\) | 2. | \(2~\text{V}, 0.4 ~\Omega\) |
| 3. | \(>2~\text{V}, 0.5 ~\Omega\) | 4. | \(>2~\text{V}, 0.4 ~\Omega\) |
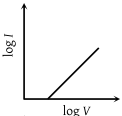
When a current I is passed through a wire of constant resistance, it produces a potential difference V across its ends. The graph drawn between log I and log V will be
(1)
(2)
(3)
(4)