The displacement \( x\) of a particle varies with time \(t\) as \(x = A sin\left (\frac{2\pi t}{T} +\frac{\pi}{3} \right)\). The time taken by the particle to reach from \(x = \frac{A}{2} \) to \(x = -\frac{A}{2} \) will be:
1.
\(\frac{T}{2}\)
2.
\(\frac{T}{3}\)
3.
\(\frac{T}{12}\)
4.
\(\frac{T}{6}\)
Force on a particle \(F\) varies with time \(t\) as shown in the given graph. The displacement \(x\) vs time \(t\) graph corresponding to the force-time graph will be:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
The time period of a simple pendulum in a stationary trolley is \(T_1.\) If the trolley is moving with a constant speed, then the time period is \(T_2.\) Then:
1. \(T_1>T _2\)
2. \(T_1<T _2\)
3. \(T_1=T _2\)
4. \(T_2= \infty \)
1. \(5~\text{Hz}\)
2. \(20~\text{Hz}\)
3. \(10~\text{Hz}\)
4. \(40~\text{Hz}\)
A particle is moving along the x-axis. The speed of particle v varies with position x as . The time period of S.H.M is
1.
2.
3.
4.
A block of mass \(m\) is attached to a massless spring of spring constant \(k,\) with the other end of the spring fixed to the wall of a trolley. Initially, the spring is unstretched, and the trolley begins to move rightward with a velocity that increases linearly with time, as shown in the velocity-time \((v\text-t)\) graph.
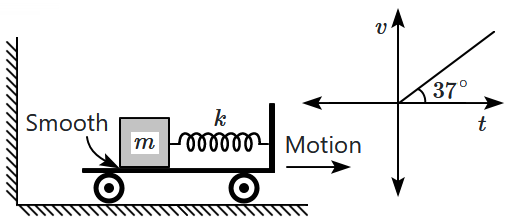
The total energy of oscillation of the block as observed from the trolley frame is:
1. \(\dfrac{32m^2}{6k}\)
2. \(\dfrac{9m^2}{8k}\)
3. \(\dfrac{9m^2}{32k}\)
4. \(\dfrac{8m^2}{9k}\)
A body of mass \(20\) g is executing SHM with amplitude \(5\) cm. When it passes through the equilibrium position its speed is \(20\) cm/s. What would be the distance from equilibrium when its speed becomes \(10\) cm/s?
1. \(\frac{5\sqrt{3}}{4}\) cm
2. \(\frac{5\sqrt{3}}{2}\) cm
3. \(\frac{25\sqrt{7}}{2}\) cm
4. \(5\sqrt{3}\) cm
For a simple harmonic oscillator, a velocity-time diagram is shown. The angular frequency of oscillation is:
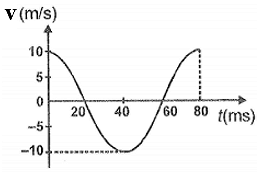
1. rad/s
2. rad/s
3. 25 rad/s
4. 25 rad/s
In an S.H.M, when the displacement is one-fourth of the amplitude, the ratio of total energy to the potential energy is
1. 16: 1
2. 1: 16
3. 1: 8
4. 8: 1
A particle executing S.H.M. Its displacement x varies with time t as The maximum velocity of the particle will be:
1. 20 unit
2. 10 unit
3. 40 unit
4. 5 unit

