| 1. |  |
2. |  |
| 3. |  |
4. |  |
| 1. | \(\frac{1}{2}\) | 2. | \(1\) |
| 3. | \(4\) | 4. | \(\frac{1}{4}\) |
A cylindrical conductor of radius \(R\) is carrying a constant current. The plot of the magnitude of the magnetic field \(B\) with the distance \(d\) from the centre of the conductor is correctly represented by the figure:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Two toroids \(1\) and \(2\) have total no. of turns \(200\) and \(100\) respectively with average radii \(40~\text{cm}\) and \(20~\text{cm}\) respectively. If they carry the same current \(i,\) what will be the ratio of the magnetic fields along the two loops?
1. \(1:1\)
2. \(4:1\)
3. \(2:1\)
4. \(1:2\)

| 1. | \(I_1=3 A\) into the paper | 2. | \(I_2=3 A\) out of the paper |
| 3. | \(I_3=0\) | 4. | \(I_3=1 A\) out of the paper |
The Ampere law is based on which theorem?
1. Green’s theorem
2. Gauss divergence theorem
3. Stoke’s theorem
4. Maxwell theorem
Rank the value of for the closed paths shown in figure from the smallest to largest:
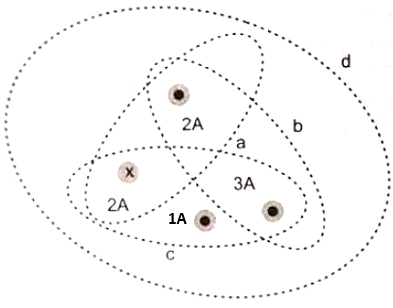
1. a, b, c, d
2. a, c, d, b
3. a, d, c, b
4. a, c, b, d
Consider the three closed loops drawn using solid line in the magnetic field (magnetic field lines are drawn using dotted line) of an infinite curent-carrying wire normal to the plane of paper as shown.
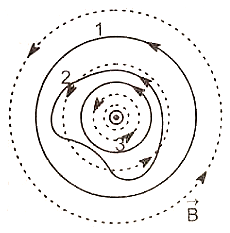
Rank the line integral of the magnetic field along each path in order of increasing magnitude:
1. 1 > 2 > 3
2. 1 = 3 > 2
3. 1 = 2 = 3
4. 3 > 2 > 1
Only the current inside the Amperian loop contributes in:
1. finding magnetic field at any point on the Ampere's loop
2. line integral of magnetic field
3. in both of the above
4. in neither of them
| (a) | \(\oint B\cdot dl= \mp 2\mu_0 I\) |
| (b) | the value of \(\oint B\cdot dl\) is independent of the sense of \(C\). |
| (c) | there may be a point on \(C\) where \(B\) and \(dl\) are perpendicular. |
| (d) | \(B\) vanishes everywhere on \(C\). |
Which of the above statements is correct?
| 1. | (a) and (b) | 2. | (a) and (c) |
| 3. | (b) and (c) | 4. | (c) and (d) |
