If force \(F=500-100t,\) then the function of impulse with time will be:
1. \( 500 t-50 t^2 \)
2. \( 50 t-10 \)
3. \( 50-t^2 \)
4. \( 100 t^2\)
A particle of mass m is tied to a string of length \(l\) and whirled into a horizontal plane. If the tension in the string is T, then the speed of the particle will be:
1.
2.
3.
4.
A small ball is suspended from a thread. If it is lifted up with an acceleration of \(4.9\) ms–2 and lowered with an acceleration of \(4.9\) ms–2, then the ratio of the tension in the thread in both cases will be:
1. \(1:3\)
2. \(3:1\)
3. \(1:1\)
4. \(1:5\)
If a ladder is not in a balanced condition against a smooth vertical wall, then it can be brought to a balanced condition by:
| 1. | decreasing the length of the ladder. |
| 2. | increasing the length of the ladder. |
| 3. | increasing the angle of inclination. |
| 4. | decreasing the angle of inclination. |
For rocket propulsion, the velocity of exhaust gases relative to the rocket is \(2\) km/s. If the mass of a rocket system is \(1000\) kg, then the rate of fuel consumption for the rocket to rise with an acceleration \(4.9\) m/s2 will be:
1. \(12.25~\text{kg}/\text{s} \)
2. \(17.5~\text{kg}/\text{s} \)
3. \(7.35~\text{kg}/\text{s} \)
4. \(5.2~\text{kg}/\text{s} \)
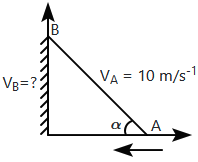
A rigid rod is placed against the wall as shown in the figure. When the velocity at its lower end is \(10\) ms-1 and its base makes an angle \(\alpha=60^\circ\) with horizontal, then the vertical velocity of its end \(\mathrm{B}\) (in ms-1) will be:
| 1. | \(10\sqrt{3}\) | 2. | \(\frac{10}{\sqrt{3}}\) |
| 3. | \(5\sqrt{3}\) | 4. | \(\frac{5}{\sqrt{3}}\) |
If \(100\) N force is applied to \(10\) kg block as shown in diagram, then the acceleration produced for the slab will be:

| 1. | \(1. 65 \) m/s2 | 2. | \(0.98 \) m/s2 |
| 3. | \(1. 2 \) m/s2 | 4. | \(0.25\) m/s2 |
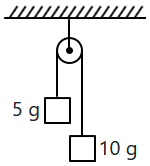
Two masses as shown are suspended from a massless pulley. What would be the acceleration of the system when masses are left free?
1. \(2g/3\)
2. \(g/3\)
3. \(g/9\)
4. \(g/7\)
(where \(g\) is the acceleration due to gravity.)
A body of mass 3 kg hits a wall at an angle of 60º & returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
1. 150 N
2. 50 N
3. 100 N
4. 75 N
A mass of 1 kg is thrown up with a velocity of 100 m/s. After 5 seconds, it explodes into two parts. One part of mass 400 g comes down with a velocity of 25 m/s. Calculate the velocity of the other part.
1. 40 m/s upward
2. 40 m/s downward
3. 100 m/s upward
4. 60 m/s downward