Given below are two statements:
| Assertion (A): | Position-time graph of a stationary object is a straight line parallel to the time axis. |
| Reason (R): | For a stationary object, the position does not change with time. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |
| Assertion (A): | Displacement of a body may be zero when distance travelled by it is not zero. |
| Reason (R): | The displacement is the longest distance between initial and final position. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |
A particle moves along a path \(ABCD\) as shown in the figure. The magnitude of the displacement of the particle from \(A\) to \(D\) is:
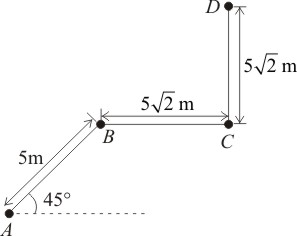
1. m
2. \(10\) m
3. m
4. \(15\) m
A drunkard walking in a narrow lane takes \(5\) steps forward and \(3\) steps backward, followed again by \(5\) steps forward and \(3\) steps backward, and so on. Each step is \(1\) m long and requires \(1\) s. There is a pit on the road \(13\) m away from the starting point. The drunkard will fall into the pit after:
1. \(37\) s
2. \(31\) s
3. \(29\) s
4. \(33\) s
The displacement \(x\) of a particle moving in one dimension under the action of a constant force is related to time \(t\) by the equation \(t=\sqrt{x}+3,\) where \(x\) is in meters and \(t\) is in seconds. What is the displacement of the particle from \(t=0~\text s\) to \(t = 6~\text s?\)
1. \(0\)
2. \(12~\text m\)
3. \(6~\text m\)
4. \(18~\text m\)
If a body travels some distance in a given time interval, then for that time interval, its:
| 1. | Average speed ≥ |Average velocity| |
| 2. | |Average velocity| ≥ Average speed |
| 3. | Average speed < |Average velocity| |
| 4. | |Average velocity| must be equal to average speed. |
A car moves from \(X\) to \(Y\) with a uniform speed \(v_u\) and returns to \(X\) with a uniform speed \(v_d.\) The average speed for this round trip is:
| 1. | \(\dfrac{2 v_{d} v_{u}}{v_{d} + v_{u}}\) | 2. | \(\sqrt{v_{u} v_{d}}\) |
| 3. | \(\dfrac{v_{d} v_{u}}{v_{d} + v_{u}}\) | 4. | \(\dfrac{v_{u} + v_{d}}{2}\) |
The figure gives the \((x\text-t)\) plot of a particle in a one-dimensional motion. Three different equal intervals of time are shown. The signs of average velocity for each of the intervals \(1,\) \(2\) and \(3,\) respectively are:

| 1. | \(-,-,+\) | 2. | \(+,-,+\) |
| 3. | \(-,+,+\) | 4. | \(+,+,-\) |
A vehicle travels half the distance \(L\) with speed \(v_1\) and the other half with speed \(v_2,\) then its average speed is:
| 1. | \(\dfrac{v_{1} + v_{2}}{2}\) | 2. | \(\dfrac{2 v_{1} + v_{2}}{v_{1} + v_{2}}\) |
| 3. | \(\dfrac{2 v_{1} v_{2}}{v_{1} + v_{2}}\) | 4. | \(\dfrac{L \left(\right. v_{1} + v_{2} \left.\right)}{v_{1} v_{2}}\) |
The coordinate of an object is given as a function of time by \(x = 7 t - 3 t^{2}\), where \(x\) is in metres and \(t\) is in seconds. Its average velocity over the interval \(t=0\) to \(t=4\) is will be:
1. \(5\) m/s
2. \(-5\) m/s
3. \(11\) m/s
4. \(-11\) m/s
