Given below are two statements:
| Assertion (A): | Position-time graph of a stationary object is a straight line parallel to the time axis. |
| Reason (R): | For a stationary object, the position does not change with time. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
A particle moves along a path \(ABCD\) as shown in the figure. The magnitude of the displacement of the particle from \(A\) to \(D\) is:
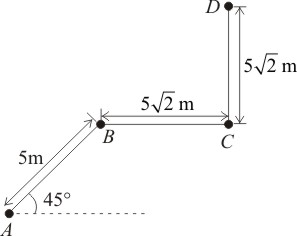
1. m
2. \(10\) m
3. m
4. \(15\) m

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
A drunkard walking in a narrow lane takes \(5\) steps forward and \(3\) steps backward, followed again by \(5\) steps forward and \(3\) steps backward, and so on. Each step is \(1\) m long and requires \(1\) s. There is a pit on the road \(13\) m away from the starting point. The drunkard will fall into the pit after:
1. \(37\) s
2. \(31\) s
3. \(29\) s
4. \(33\) s

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
If a body travels some distance in a given time interval, then for that time interval, its:
| 1. | Average speed ≥ |Average velocity| |
| 2. | |Average velocity| ≥ Average speed |
| 3. | Average speed < |Average velocity| |
| 4. | |Average velocity| must be equal to average speed. |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
A car moves from \(X\) to \(Y\) with a uniform speed \(v_u\) and returns to \(X\) with a uniform speed \(v_d.\) The average speed for this round trip is:
| 1. | \(\dfrac{2 v_{d} v_{u}}{v_{d} + v_{u}}\) | 2. | \(\sqrt{v_{u} v_{d}}\) |
| 3. | \(\dfrac{v_{d} v_{u}}{v_{d} + v_{u}}\) | 4. | \(\dfrac{v_{u} + v_{d}}{2}\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
The figure gives the \((x\text-t)\) plot of a particle in a one-dimensional motion. Three different equal intervals of time are shown. The signs of average velocity for each of the intervals \(1,\) \(2\) and \(3,\) respectively are:

| 1. | \(-,-,+\) | 2. | \(+,-,+\) |
| 3. | \(-,+,+\) | 4. | \(+,+,-\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
The coordinate of an object is given as a function of time by \(x = 7 t - 3 t^{2}\), where \(x\) is in metres and \(t\) is in seconds. Its average velocity over the interval \(t=0\) to \(t=4\) is will be:
1. \(5\) m/s
2. \(-5\) m/s
3. \(11\) m/s
4. \(-11\) m/s

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
A particle moving in a straight line covers half the distance with a speed of \(3~\text{m/s}\). The other half of the distance is covered in two equal time intervals with speeds of \(4.5~\text{m/s}\) and \(7.5~\text{m/s}\) respectively. The average speed of the particle during this motion is:
1. \(4.0~\text{m/s}\)
2. \(5.0~\text{m/s}\)
3. \(5.5~\text{m/s}\)
4. \(4.8~\text{m/s}\)

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
The displacement \((x)\) of a point moving in a straight line is given by; \(x=8t^2-4t.\) Then the velocity of the particle is zero at:
| 1. | \(0.4~\text s\) | 2. | \(0.25~\text s\) |
| 3. | \(0.5~\text s\) | 4. | \(0.3~\text s\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
If the velocity of a particle is \(v=At+Bt^{2},\) where \(A\) and \(B\) are constants, then the distance travelled by it between \(1~\text{s}\) and \(2~\text{s}\) is:
| 1. | \(3A+7B\) | 2. | \(\frac{3}{2}A+\frac{7}{3}B\) |
| 3. | \(\frac{A}{2}+\frac{B}{3}\) | 4. | \(\frac{3A}{2}+4B\) |

To unlock all the explanations of this course, you need to be enrolled.

To unlock all the explanations of this course, you need to be enrolled.
