A straight wire of mass \(200~\text{g}\) and length \(1.5~\text{m}\) carries a current of \(2~\text{A}\). It is suspended in mid-air by a uniform horizontal magnetic field \(B\) (shown in the figure). What is the magnitude of the magnetic field?

1. \(0.65~\text{T}\)
2. \(0.77~\text{T}\)
3. \(0.44~\text{T}\)
4. \(0.20~\text{T}\)

In a region of space, magnetic field is parallel to the positive y-axis and the charged particle is moving along the positive x-axis (as shown in the figure). The directions of Lorentz force for an electron (negative charge) and proton (positive charge) are respectively:

1. -z-axis, +z-axis

2. +z-axis, -z-axis

3. -z-axis, -z-axis

4. +z-axis, +z-axis

The radius of the path of an electron and frequency (mass $9\times {10}^{-31} \mathrm{kg}$ and charge $1.6\times {10}^{-19} \mathrm{C}$) moving at a speed of \(3\times10^7\) m/s in a magnetic field of \(6\times10^{-4}\) T perpendicular to it are respectively:
1. \(24\) cm, \(4\) MHz
2. \(22\) cm, \(4\) MHz
3. \(28\) cm, \(2\) MHz
4. \(26\) cm, \(2\) MHz

An electron $\left(mass 9\times {10}^{-31} kg and charge 1.6\times {10}^{-19} C\right)$ is moving at a speed of 3 ×10⁷ m/s in a magnetic field perpendicular to it. The energy of the electron in keV is: ( 1 eV = 1.6 × 10^–19 J)

1. 2.5 keV

2. 3.5 keV

3. 20 keV

4. 3.0 keV

An element \(\Delta l=\Delta x \hat{i}\) is placed at the origin and carries a large current of \(I=10\) A (as shown in the figure). What is the magnetic field on the y-axis at a distance of \(0.5\) m?(\(\Delta x=1~\mathrm{cm}\))
       

A straight wire carrying a current of 12 A is bent into a semi-circular arc of radius 2.0 cm as shown in the figure. Considering the magnetic field B at the centre of the arc, what will be the magnetic field due to the straight segments?

$1. 0$
$2. 1.2\times {10}^{-4} T$
$3. 2.1\times {10}^{-4} T$
$4. None of these$

A straight wire carrying a current of 12 A is bent into a semi-circular arc of radius 2.0 cm as shown in the figure. Consider the magnetic field B at the centre of the arc. What is the magnetic field at centre due to the semi-circular loop?

$1. 0$
$2. 3.8\times {10}^{-4} T$
$3. 1.9\times {10}^{-4} T$
$4. 2.9\times {10}^{-4} T$

Consider a tightly wound \(100\) turn coil of radius \(10\) cm, carrying a current of \(1\) A. What is the magnitude of the magnetic field at the centre of the coil?
1. \(8.2\times10^{-4}\) T
2. \(4.6\times10^{-4}\) T
3. \(5.2\times10^{-4}\) T
4. \(6.2\times10^{-4}\) T

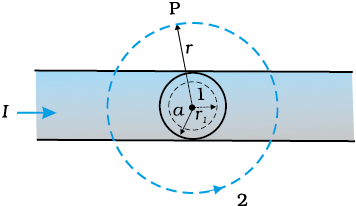
The figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. If the magnetic field in the region (r < a) is $B_1$ and for (r > a) is $B_2$, then $\frac{B_1}{B_2}$ is:

$1. \frac{a}{r}$
$2. \frac{a^2}{r^2}$
$3. \frac{r^2}{a^2}$
$4. \frac{r}{a}$

A solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns. It carries a current of 5 A. What is the magnitude of the magnetic field inside the solenoid?

$1. 6.28\times {10}^{-3} T$
$2. 3.14\times {10}^{-3} T$
$3. 2.72\times {10}^{-3} T$
$4. 5.17\times {10}^{-3} T$