Ncert Exercises & Solutions

4.31 A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?

NEETprep Answer:

Speed of the cyclist, $v = 27 km / h = 7.5 m / s$

Radius of the circular turn, r = 80 m

Centripetal acceleration is given as:

$a_{c} = \frac{v^{2}}{r}$
$= \frac{{(7.5)}^{2}}{80} = 0.7 m / s^{2}$

The situation is shown in the given figure:

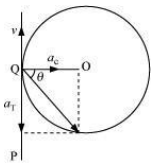
Suppose the cyclist begins cycling from point P and moves toward point Q. At point Q, he applies the breaks and decelerates the speed of the bicycle by 0.5 m/s2 .

This acceleration is along the tangent at Q and opposite to the direction of the motion of the cyclist.

Since the angle between is 90°, the resultant acceleration a is given by:

$a = \sqrt{a_{c}^{2} + a_{r}^{2}}$
$= \sqrt{{(0.7)}^{2} + {(0.5)}^{2}}$
$= \sqrt{0.74} = 0.86 m / s^{2}$
$\tan θ = \frac{a_{c}}{a_{r}}$

Where $θ$ is the angle of the resultant with the direction of velocity

$\tan θ = \frac{0.7}{0.5} = 1.4$
$θ = \tan^{- 1} (1.4) = 54.46 °$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions