Ncert Exercises & Solutions

Q 16. (a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in Fig. 6.21.

(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v= 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

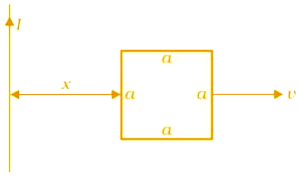
(a) Take a small element dy in the loop at a distance y from the long straight wire (as shown in the given figure).
Magnetic flux associated with the element $dy, d \emptyset = BdA$
Where, dA = Area of element dy = a dy
B = Magnetic field at distance y
$= \frac{μ_{0} I}{2 π y}$
I = Current in the win

$\begin{array}{l} μ_{0} = Permeability of free space = 4 π \times 10^{- 7} \\ ∴ dϕ = \frac{μ_{0} Ia}{2 π} \frac{dy}{y} \\ ϕ = \frac{μ_{0} Ia}{2 π} \int \frac{dy}{y} \end{array}$

v tends from x to a + x.

$\begin{array}{l} ∴ ϕ = \frac{μ_{0} Ia}{2 π} \int_{x}^{a + y} \frac{dy}{y} \\ = \frac{μ_{0} Ia}{2 π} [\log_{e} y]_{x}^{a + x} \\ = \frac{μ_{0} Ia}{2 π} \log_{e} (\frac{a + x}{x}) \end{array}$

For mutual inductance M, the flux is given as:

$\begin{array}{l} ϕ = MI \\ ∴ MI = \frac{μ_{0} Ia}{2 π} \log_{e} (\frac{a}{x} + 1) \\ M = \frac{μ_{0} a}{2 π} \log_{e} (\frac{a}{x} + 1) \end{array}$

(b) Emfinduced in the loop, e = B'av

$\begin{array}{l} = (\frac{μ_{0} I}{2 πx}) av \\ Given, I = 50 A \\ x = 0 .2 m \\ a = 0 .1 m \\ v = 10 m / s \\ e = \frac{4 π \times 10^{- 7} \times 50 \times 0 .1 \times 10}{2 π \times 0 .2} \\ e = 5 \times 10^{- 5} V \end{array}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions