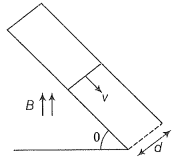
Hint: The change in the magnetic flux results in the acceleration of the wire.
Step 1: Here, the component of the magnetic field perpendicular to the plane=
Now, the conductor moves with speed v perpendicular to component of magnetic field. This causes motional emf across two ends of rod, which is given =v()d
This makes the flow of induced current, where, R is the resistance of rod. Now, current carrying rod experience force which is given by F=iBd (horizontally in backward direction).
Now, the component of magnetic force parallel to incline plane along upward direction=
Step 2: Also, the component of weight (mg) parallel to inclined plane along downward direction=mg sin
Now, by Newton's second law of motion;
Step 3: But, this is the linear differential equation.
On solving, we get;