Ncert Exercises & Solutions

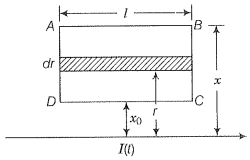
Consider an infinitely long wire carrying a current I(t), with $\frac{dI}{dt} = λ$ =constant. Find the current produced in the rectangular loop of wire ABCD if its resistance is R (figure).

Hint: The change in current results in a change in magnetic field through the loop.

Step 1 : Let us consider a strip of length l and width dr at a distance r from infinite long current carrying

wire . The magnetic field at strip due to current carrying wire is given by;

Field, B (r) = \frac{μ_{0} I}{2 πr} (out of paper)

Step 2 : Total flux through the loop is;

Flux = \frac{μ_{0} I}{2 π} l \int_{x_{0}}^{x} \frac{dr}{r} = \frac{μ_{0} Il}{2 π} \ln (\frac{x}{x_{0}}) . . . (i)

Step 3 : The emf inuced can be obtained by differentiating the eq . (i) w . r . t . t and then applying Ohm' s law;

\frac{ε}{R} = I

We have, induced current = \frac{1}{R} \frac{dφ}{dt} = \frac{ε}{R} = \frac{μ_{0} Il}{2 π} \frac{λ}{R} \ln (\frac{x}{x_{0}}) (∵ \frac{dI}{dt} = λ)

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions