Ncert Exercises & Solutions

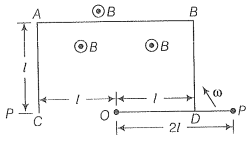
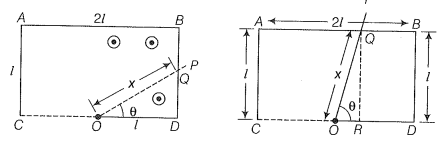
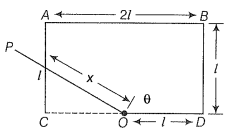
ODBAC is a fixed rectangular conductor of negligible resistance (CO is not connected) and OP is a conductor which rotates clockwise with angular velocity $ω$ (figure). The entire system is in uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electric contact with ABDC. The rotating conductor has a resistance of $λ$ per unit length. Find the current in the rotating conductor, as it rotates by $180 °$ .

Hint: The cutting of the magnetic field results in induced emf.

Step 1:

Let us consider the position of rotating conductor at time interval

t = 0 to t = \frac{π}{4 ω} (or T / 8);

the rod OP will make contact with the side BD . Let the length OQ of the contact at sometime t

such that 0 < t < \frac{π}{4 ω} or 0 < t < \frac{T}{8} be x . The flux through the area ODQ is;

ϕ = B \frac{1}{2} QD \times OD = B \frac{1}{2} ltanθ \times l

= \frac{1}{2} {Bl}^{2} tanθ, where θ = ω

Step 2 : Applying Faraday' s law of EMI,

Thus, the magnitude of the emf generated is ε = \frac{dϕ}{dt} = \frac{1}{2} {Bl}^{2} {ωsec}^{2} ωt

The current is I = \frac{ε}{R} where R is the resistance of the rod in contact .

Where, R \propto λ

R = λx = \frac{λl}{cosωt}

∴ I = \frac{1}{2} \frac{{Bl}^{2} ω}{λl} \sec^{2} ωtcosωt = \frac{Blω}{2 λcosωt}

Step 3 : Let the length OQ of the contact at some time t such that \frac{π}{4 ω} < t < \frac{3 π}{4 ω} or \frac{T}{8} < t < \frac{3 T}{8} be x .

The rod is in contact with the side AB . The flux through the area OQBD is :

ϕ = (l^{2} + \frac{1}{2} \frac{l^{2}}{tanθ}) B

where, θ = ωt

Thus, the magnitude of emf generated in the loop is :

ε = \frac{dφ}{dt} = \frac{1}{2} {Bl}^{2} ω \frac{\sec^{2} ωt}{\tan^{2} ωt}

The current is I = \frac{ε}{R} = \frac{ε}{λx} = \frac{εsinωt}{λl} = \frac{1}{2} \frac{Blω}{λsinωt}

Similarly for \frac{3 π}{4 ω} < t < \frac{π}{ω} or \frac{3 T}{8} < t < \frac{T}{2}, the rod will be in touch with AC .

Step 4 : The flux through OQABD is given by :

ϕ = (2 l^{2} - \frac{l^{2}}{2 \tan ωt}) B

And the magnitude of emf generated in loop is given by :

ε = \frac{dϕ}{dt} = \frac{{Rωl}^{2} \sec^{2} ωt}{2 \tan^{2} ωt}

l = \frac{ε}{R} = \frac{ε}{λx} = \frac{1}{2} \frac{Blω}{λsinωt}

These are the required expressions .

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions