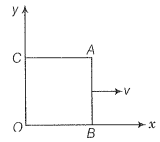
A magnetic field covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d (figure). The wires are in the x-y plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit? What is the force needed to keep the wire moving at constant velocity?

© 2026 GoodEd Technologies Pvt. Ltd.