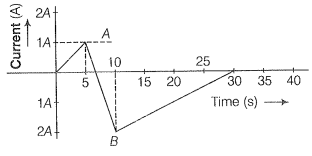
A (current versus time) graph of the current passing through a solenoid is shown in the figure. For which time is the back electromotive force (u) a maximum. If the back emf at t=3 s is e, find the back emf at t=7 s, 15s and 40 s. OA, AB and BC are straight line segments.

© 2026 GoodEd Technologies Pvt. Ltd.