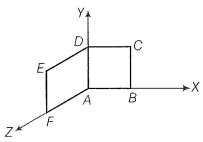
A loop, made of straight edges has six corners at A(0, 0, 0), B(L, 0, 0), C(L, L, 0), D(0, L, 0), E(0, L, L) and F(0, 0, L). A magnetic field B= T is present in the region. The flux passing through the loop ABCDEFA (in that order) is:
1. B0L2 Wb3
2. 2B0L2 Wb
3. \(\sqrt2\)B0L2 Wb
4. 4B0L2 Wb

© 2026 GoodEd Technologies Pvt. Ltd.