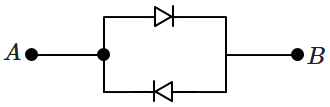
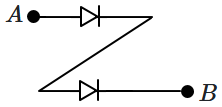
Physics - Section A
1. Given below are two statements:
| Assertion (A): |
During the process of refraction, the frequency of light changes as it travels from one medium to another. |
| Reason (R): |
As light undergoes refraction, and travels from one medium to another, the refractive index changes and the speed of light also changes. |
| 1. |
Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. |
(A) is True but (R) is False. |
| 4. |
(A) is False but (R) is True. |
2. If two dispersive prisms are combined so their bases are parallel and on the same plane, the net angle of dispersion (due to both of them) will be equal to:
| 1. |
the sum of individual angles of dispersion |
| 2. |
the difference of individual angles of dispersion |
| 3. |
the average of individual angles of dispersion |
| 4. |
the half of difference of individual angles of dispersion |
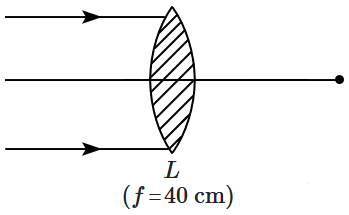
3. A parallel beam of light is incident onto a convex lens of focal length
\(40~\text{cm},\) parallel to its principal axis. A thin prism, that introduces a deviation of
\(0.01\) radian is introduced into the path of incident light on the lens, placed normal to the light. The final image is displaced by:
| 1. |
\(0.4~\text{cm}\) to right along the principal axis |
| 2. |
\(0.4~\text{cm}\) to the left along the principal axis |
| 3. |
\(0.4~\text{cm}\) perpendicular to the principal axis |
| 4. |
zero, it is formed in the same position as before |
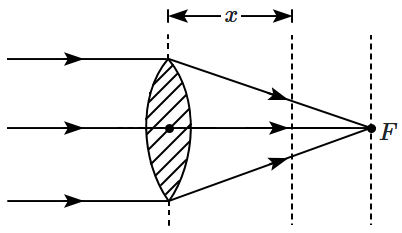
4. A parallel beam of light is brought to focus on its axis at
\(F,\) by a lens, as shown in the figure. The focal length of the lens is
\(f.\) The intensity of the refracted beam is proportional to:
(
\(x\) is the distance from lens where intensity is measured)
| 1. |
\(x^2\) |
2. |
\({\dfrac{1}{ x^2}}\) |
| 3. |
\((f-x)^2\) |
4. |
\({\dfrac{1}{(f-x)^2}}\) |
5. Given below are two statements:
| Assertion (A): |
Magnifying power of a simple microscope is minimum when it is used in normal adjustment. |
| Reason (R): |
During normal adjustment, the object distance is maximum, so magnifying power is minimum. |
| 1. |
Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. |
(A) is True but (R) is False. |
| 4. |
Both (A) and (R) are False. |
6. A system of lenses is used to observe the image of an object in front of it. A glass slab
\((\mu=1.5)\) of thickness
\(6~\text{cm}\) is placed between the object and the lenses. In order to observe the image at the same position, the object has to be moved:
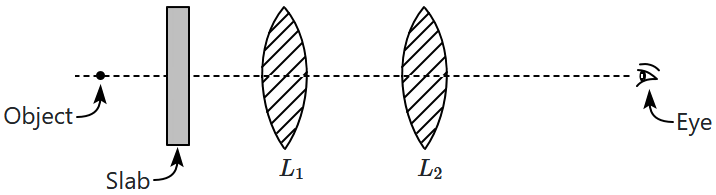
| 1. |
towards the slab by \(4~\text{cm}\) |
| 2. |
towards the slab by \(2~\text{cm}\) |
| 3. |
away from the slab by \(4~\text{cm}\) |
| 4. |
away from the slab by \(2~\text{cm}\) |
7. Light is incident onto the surface
\(AB\) of a right-angled
\((\angle A=90^\circ)\) isosceles prism, kept in air.
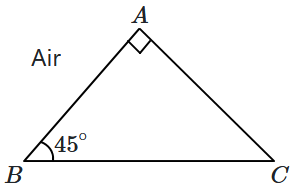
What should be the maximum refractive index of the material of the prism, if a ray incident normally on
\(AB\) does not undergo total internal reflection on the base
\(BC\)?
| 1. |
\(2\) |
2. |
\(\sqrt2\) |
| 3. |
\(\begin{aligned}\frac{2}{\sqrt3} & \\ \end{aligned}\) |
4. |
\(\sqrt3\) |
8. If an object is placed under water \(\left ( \text{refractive index}=\frac{4}{3} \right )\) at a depth \(d\) below the surface, and viewed from above, it would appear to be at a depth:
1. \(d\)
2. \(\large\frac{d}{3}\)
3. \(\large\frac{3d}{4}\)
4. \(\large\frac{4d}{3}\)
9. \(\mathrm{n}\)-type silicon is made by doping silicon crystals with:
| 1. |
phosphorus atoms |
| 2. |
carbon atoms |
| 3. |
electrons in valence band |
| 4. |
protons in conduction band |
10. An LED is:
| 1. |
a \(\mathrm{p}\)-doped silicon that emits light |
| 2. |
a \(\mathrm{n}\)-doped silicon that emits light |
| 3. |
a \(\mathrm{p \text-n}\) diode that emits light |
| 4. |
a transistor that absorbs light |
11. A NAND and a NOR gate are connected in series, as follows:

The output
\(Y\) is equal to:
1.
\(A\) AND
\(B\)
2.
\(A\) OR
\(B\)
3.
\(A\) NAND
\(B\)
4.
\(A\) NOR
\(B\)
12. The diode
\(D\) has a very small resistance. The applied voltage
\(V_{AB}=V_0\sin\omega t~~~~(V_0=5~\text{V},\omega=100~\text s^{-1}).\) After switching on the circuit, a steady state behaviour is reached. Which, of the following, is the best explanation of what happens?
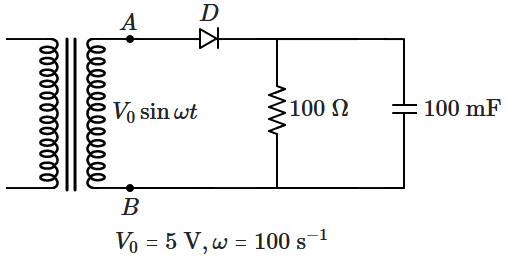
| 1. |
The \(100~\text{mF}\) capacitor charges to \(+5~\text V,\) and then provides an almost steady-current through the \(100~\Omega\) resistance |
| 2. |
The \(100~\text{mF}\) capacitor charges and discharges when \(\text{AC}\) flows through it, the average voltage across it being zero. |
| 3. |
Current flows through the \(100~\Omega\) resistor forward and backward. |
| 4. |
The diode does not work due to the capacitor. |
13. A
\(\mathrm{p\text-n}\) junction diode is said to be forward-biased when:
| 1. |
current flows from \(\mathrm{p}\) to \(\mathrm{n}\) |
| 2. |
current flows from \(\mathrm{n}\) to \(\mathrm{p}\) |
| 3. |
current flows into \(\mathrm{p}\) and current also flow into \(\mathrm{n}\) |
| 4. |
electron flow into \(\mathrm{p}\) and electrons flow into \(\mathrm{n}\) |
14. In the circuit shown in the figure, the two diodes
\(D_1,D_2\) are considered to be ideal.
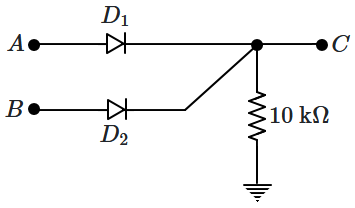
The circuit shown in the figure can be used as:
1. an AND gate
2. an OR gate
3. a NOT gate
4. an XOR gate
15. The wavefronts of a light wave travelling in vacuum are given by \(x+y+z=c\). The angle made by the direction of propagation of light with the X-axis is:
1. \(0^{\circ}\)
2. \(45^{\circ}\)
3. \(90^{\circ}\)
4. \({\cos^{-1}\left({1}/{\sqrt{3}}\right )}\)
16. Two slabs of thickness
\(t_1\) &
\(t_2\) and refractive indices
\(\mu_2\) &
\(\mu_2\) are placed normally in the path of light, travelling in air. The change in optical path due to insertion of the slabs is
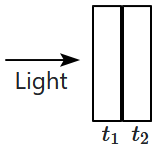
1.
\(\mu_1t_1+\mu_2t_2\)
2.
\(\dfrac{t_1}{\mu_1}+\dfrac{t_2}{\mu_2}\)
3.
\((\mu_1-1)t_1+(\mu_2-1)t_2\)
4.
\(\dfrac{t_1}{\mu_1-1}+\dfrac{t_2}{\mu_2-1}\)
17. In the YDSE setup shown in the figure, if
\(P\) is the point on the screen in front of mid-point between slits, then:
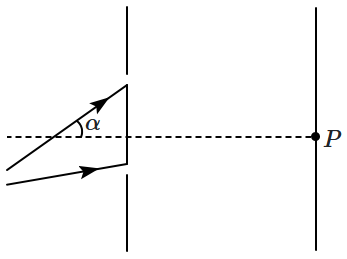
| 1. |
zero-order maximum will lie above point \(P\) |
| 2. |
zero-order maximum will lie at point \(P\) |
| 3. |
zero-order maximum will lie below point \(P\) |
| 4. |
zero-order maximum may lie above or below point \(P\) |
18. Interference fringes are formed on a screen placed perpendicular to a mirror
\((AB)\) at end
\(B,\) due to light from a point source
\(S,\) located at a distance
\('d'\) in front of the mirror (width
\(=D\)). The wavelength of light is
\(\lambda.\) The distance of the first maximum from
\(B\) is
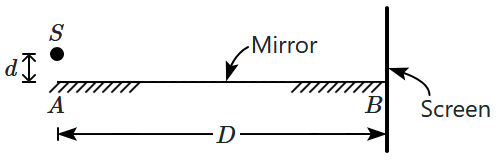
1.
\(\dfrac{\lambda D}{d}\)
2.
\(\dfrac{\lambda D}{2d}\)
3.
\(\dfrac{2\lambda D}{d}\)
4.
\(\dfrac{\lambda D}{4d}\)
19. Given below are two statements:
| Assertion (A): |
Radio waves can be polarised. |
| Reason (R): |
Sound waves in the air are longitudinal in nature. |
| 1. |
Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. |
(A) is True but (R) is False. |
| 4. |
Both (A) and (R) are False. |
20. A photon of energy
\(10.2\) eV corresponds to light of wavelength
\(\lambda_0\). Due to electron transition from
\(n = 2 \) to
\(n = 1\) in a hydrogen atom, light of wavelength
\(\lambda\) is emitted. If we take into account the recoil of atom when photon is emitted then:
| 1. |
\(\lambda = \lambda_0\) |
| 2. |
\(\lambda < \lambda_0\) |
| 3. |
\(\lambda > \lambda_0\) |
| 4. |
data is not sufficient to reach a conclusion |
21. The electric field of light wave is given as \(\vec{E}=10^{-3} \cos \left(\frac{2 \pi x}{5 \times 10^{-7}}-2 \pi \times 6 \times 10^{14} t\right) ~\text{N/C}\). This light falls on a metal plate of work function \(2~\text{eV}\). The stopping potential of the photo-electrons is: \(\left(\text{Given,}~{E}~(\text {in } \text{eV})=\frac{12375}{\lambda~(\text{in } \mathring{\text{A}})}\right )\)
1. \(0.72~\text{V}\)
2. \(2.0~\text{V}\)
3. \(0.48~\text{V}\)
4. \(2.48~\text{V}\)
22. A charged particle is observed to move in a circular orbit within a uniform magnetic field. The flux of the magnetic field through the orbit of the particle is \(\phi_B.\) The orbital circumference covers two de-Broglie wavelengths.
The charge of the particle is
1. \(\frac{2h}{\phi_B}\)
2. \(\frac{h}{2\phi_B}\)
3. \(\frac{h}{\phi_B}\)
4. \(\frac{\sqrt2h}{\phi_B}\)
23. Two light sources emit
\(\mathrm{X}\)-rays with a wavelength of
\(1~\text{nm}\) and visible light with a wavelength of
\(500~\text{nm},\) respectively. Both sources emit light with the same power of
\(200~\text W.\) What is the ratio of the number density of photons of
\(\mathrm{X}\)-rays to the number density of photons of visible light for the given wavelengths?
| 1. |
\( \dfrac{1}{500} \) |
2. |
\( 500 \) |
| 3. |
\( \dfrac{1}{250} \) |
4. |
\( 250\) |
24. In a photoelectric effect experiment, the graph of stopping potential \(V\) versus reciprocal of wavelength obtained is shown in the figure. As the intensity of incident radiation is increased:

| 1. |
slope of the straight line get more steep. |
| 2. |
straight line shifts to the right. |
| 3. |
graph does not change. |
| 4. |
straight line shifts to the left. |
25. In a photoelectric experiment, blue light is capable of ejecting a photoelectron from a specific metal while green light is not able to eject a photoelectron. Ejection of photoelectrons is also possible using light of the colour:
| 1. |
yellow |
2. |
red |
| 3. |
violet |
4. |
orange |
26. In a photoelectric effect experiment, the threshold wavelength of light is \(380~\text{nm}\). If the wavelength of incident light is \(260~\text{nm}\), the maximum kinetic energy of emitted electrons will be:
Given: \(E(\text {in}~\text{eV})=\dfrac{1237}{\lambda(\text {in}~ \text{nm})}\)
1. \(3.0~\text{eV}\)
2. \(1.5~\text{eV}\)
3. \(4.5~\text{eV}\)
4. \(15.1~\text{eV}\)
27. Radiation of wavelength
\(280~\text{nm}\) is used in an experiment of photoelectric effect with cathode of work function,
\(2.5~\text{eV}.\) The maximum kinetic energy of the photoelectrons is:
(take
\(h=6.62\times10^{-34}~\text{J s}\) and
\(c=3\times10^{8}~\text{ms}^{-1}\))
| 1. |
\(4.4~\text{eV}\) |
2. |
\(7.103\times10^{-15}~\text{J}\) |
| 3. |
\(1.9~\text{eV}\) |
4. |
\(4.60~\text{eV}\) |
28. The de-Broglie wavelength of an electron having a kinetic energy \(E_K\) is given by the expression; \(\lambda_{dB}={\large\frac{12.4}{\sqrt{E_k}}}\mathring{A} .\)
In this expression, the kinetic energy is substituted in \(\text {eV}\) (numerically), and it is not very large \(\Big(\text{i.e., }E_k\ll10^{6}\Big).\)
What is the de-Broglie wavelength of \(4~\text {eV}\)-electron?
1. \(12.4~\mathring{A}\)
2. \(6.2~\mathring{A}\)
3. \(3.1~\mathring{A}\)
4. \(0.8~\mathring{A}\)
29. Particles used in Rutherford's scattering experiment to deduce the structure of atoms:
| 1. |
had atomic number \(2\) and were fully ionized. |
| 2. |
had atomic number \(2\) and were neutral. |
| 3. |
had atomic number \(4\) and were fully ionized. |
| 4. |
had atomic number \(4\) and were neutral. |
30. Given below are two plots:
| 1. |
Orbital radius \((r)\) versus the square of the principal quantum number \((n^2)\) |
| 2. |
Time period \((T)\) versus the cube of the principal quantum number \((n^3)\) |
Based on these plots, the electron's velocity in the ground state of a hydrogen atom can be determined. What is the velocity of the electron?
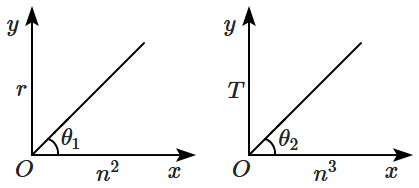
| 1. |
\(\dfrac{2\pi\theta_1}{\tan\theta_2}\) |
2. |
\(\dfrac{2\pi\tan\theta_1}{\tan\theta_2}\) |
| 3. |
\(\dfrac{2\pi\sin\theta_1}{\cos\theta_2}\) |
4. |
\(\dfrac{2\pi\tan\theta_2}{\tan\theta_1}\) |
31. In a sample of hydrogen atoms, one atom goes through a transition
\(n=3\rightarrow\) ground state with emitted wavelength
\(\lambda_1\). Another atom goes through a transition
\(n=2\rightarrow\) ground state with emitted wavelength
\(\lambda_2\) . The ratio of
\(\dfrac{\lambda_1}{\lambda_2}=\)
| 1. |
\(\dfrac{6}{5}\) |
2. |
\(\dfrac{5}{6}\) |
| 3. |
\(\dfrac{27}{32}\) |
4. |
\(\dfrac{32}{27}\) |
32. Which of the following relation is true for revolving electrons around the nucleus?
1. \(K . E=|P . E |\)
2. \( K . E=\dfrac{P . E }{2}\)
3. \(K . E=|T . E | \)
4. \( P . E=-\dfrac{K . E }{2} \)
33. The ratio of the mass densities of the nuclei \({ }^{40} \mathrm{Ca}\) and \({ }^{16} \mathrm{O}\) is close to:
| 1. |
\(0.1\) |
2. |
\(2\) |
| 3. |
\(5\) |
4. |
\(1\) |
34. Nuclear forces are:
| 1. |
short range and charge dependent |
| 2. |
short range and charge independent |
| 3. |
long range and charge dependent |
| 4. |
long range and charge independent |
Physics - Section B
35. A radioactive nucleus \(A\) with mass number \(180\) and atomic number \(72\) undergoes a series of decays:
\(A\xrightarrow{~~~\alpha~~~}A_1\xrightarrow{~~~\beta^-~~~}A_2\xrightarrow{~~~\alpha~~~}A_3\xrightarrow{~~~\gamma~~~}A_4\)
What are the mass number and atomic number, respectively, of \(A_4\text{?}\)
1. \(172\) and \(69\)
2. \(174\) and \(70\)
3. \(176\) and \(69\)
4. \(176\) and \(70\)
36. In a nuclear reaction,
\(2~\text{amu}\) of mass is converted into energy. According to Einstein's mass-energy relationship, the energy released is:
| 1. |
\(1863~\text{J}\) |
2. |
\(931.5~\text{MeV}\) |
| 3. |
\(1863~\text{MeV}\) |
4. |
\(931.5~\text{J}\) |
37. Given below are two statements:
| Assertion (A): |
The resistivity of silicon, a semiconductor, decreases when its temperature is raised. |
| Reason (R): |
When temperature is raised, the number of electrons in the conduction band as also the number of holes in the valence band increase due to transition of electrons from valence band to the conduction band. |
| 1. |
Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. |
(A) is True but (R) is False. |
| 4. |
(A) is False but (R) is True. |
38. Which one of the following statements, with respect to a semiconducting material, is not correct?
| 1. |
They have a negative temperature coefficient of resistance. |
| 2. |
They have a moderate forbidden energy gap. |
| 3. |
Current is carried by both, electrons and holes. |
| 4. |
Every semiconducting material is a tetravalent element. |
39. Which of the following is correct for the Zener diode?
| (a) |
It acts as a voltage regulator. |
| (b) |
It is used in forward bias. |
| (c) |
It is used in reverse bias. |
| (d) |
It is used as a switch in series. |
Choose the correct option from the given ones:
| 1. |
(a) and (d) |
| 2. |
(b) and (c) |
| 3. |
(a) and (c) |
| 4. |
(b) and (d) |
40. Match List I with List II.
| List I |
List II |
| (a) |
Rectifier |
(i) |
Used either for stepping up or stepping down the AC voltage. |
| (b) |
Stabilizer |
(ii) |
Used to convert AC voltage into DC voltage. |
| (c) |
Transformer |
(iii) |
Used to remove any ripple in the rectified output voltage. |
| (d) |
Filter |
(iv) |
Used for constant output voltage even when the input voltage or load current changes. |
Choose the correct option from the given ones:
| 1. |
(a)–(ii), (b)–(iv), (c)–(i), (d)–(iii) |
| 2. |
(a)–(iii), (b)–(iv), (c)–(i), (d)–(ii) |
| 3. |
(a)–(ii), (b)–(i), (c)–(iv), (d)–(iii) |
| 4. |
(a)–(ii), (b)–(i), (c)–(iii), (d)–(iv) |
41. A circuit has two
\(\mathrm{p\text-n}\) junctions which are to be connected in series or in parallel. Which connection will allow current to flow through whether
\(V_A>V_B\) or
\(V_B>V_A\)?
42. An input signal to a logic circuit's inputs is represented by a
\(0,\) if the voltage is low (true) and by a
\(1,\) if the voltage is high (false). The truth table representing the operation of the circuit is given by:
\(\begin{array}{|c|c|c|} \hline A & B & Y~\text{(output)} \\ \hline 0 & 0 & 0 \\ \hline 0 & 1 & 1 \\ \hline 1 & 0 & 0 \\ \hline 1 & 1 & 0 \\ \hline \end{array}\)
An input consisting of the following is presented to the pins
\(A\) and
\(B\):
| 1. |
pin A: \(0110101001\) |
| 2. |
pin B: \(1000011100\) |
The output
\(Y\) is:
| 1. |
\(0110100001\) |
| 2. |
\(1000010100\) |
| 3. |
\(0111100011\) |
| 4. |
\(1001010010\) |
43. In the circuit containing an ideal diode, as shown in the figure, the average power dissipated through the resistor in one cycle is:
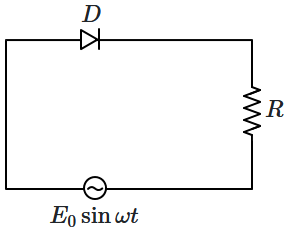
1. zero
2.
\(E^2_0\over R\)
3.
\(E^2_0\over 2R\)
4.
\(E^2_0\over 4R\)
44. The equivalent resistance between
\(A\) and
\(B\) of the network shown below is:
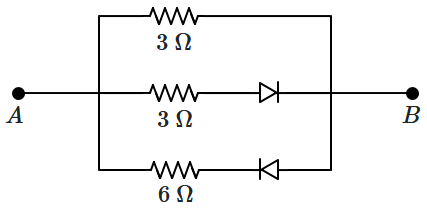
| 1. |
\(1.2~ \Omega\) |
| 2. |
\(3 ~\Omega\) |
| 3. |
\(1.5~\Omega\) if \(V_{A}>V_{B}\) and \(2~\Omega\) if \(V_{A}<V_{B}\) |
| 4. |
\(1.5~\Omega\) if \(V_{A}<V_{B}\) |
45. A narrow beam of light emerges from a source
\(S,\) gets reflected at
\(O\) from a plane mirror
\(MN,\) and forms a spot
\((P)\) on a wall, parallel to
\(MN.\) The distance between
\(S\) and the mirror is
\(40~\text{cm},\) and between the mirror and the wall is
\(60~\text{cm}.\) The mirror
\((MN)\) and the source
\((S)\) can rotate about axes perpendicular to the plane of the diagram. The angle of incidence of the ray
\(SO,\) on the mirror, is
\(45^\circ\) initially.
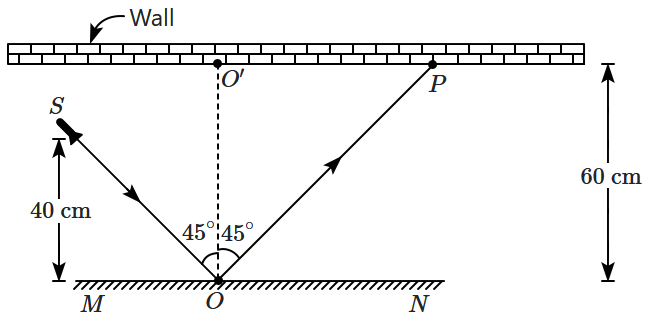
What is the distance
\(O'P\) of the spot
\((P)\) on the wall, with respect to
\(O'\) which is directly opposite to
\(O?\)
1.
\(40~\text{cm}\)
2.
\(60~\text{cm}\)
3.
\(80~\text{cm}\)
4.
\(100~\text{cm}\)
46. A narrow beam of light emerges from a source
\(S,\) gets reflected at
\(O\) from a plane mirror
\(MN,\) and forms a spot
\((P)\) on a wall, parallel to
\(MN.\) The distance between
\(S\) and the mirror is
\(40~\text{cm},\) and between the mirror and the wall is
\(60~\text{cm}.\) The mirror
\((MN)\) and the source
\((S)\) can rotate about axes perpendicular to the plane of the diagram. The angle of incidence of the ray
\(SO,\) on the mirror, is
\(45^\circ\) initially.

The mirror is fixed, but the source ray
\(SO\) rotates anticlockwise with an angular speed
\(10^{-2}~\text{rad/s}\) about
\(S.\) The angular speed of the reflected ray
\(OP\) is:
1.
\(10^{-2}~\text{rad/s}\) anticlockwise
2.
\(2\times10^{-2}~\text{rad/s}\) anticlockwise
3.
\(10^{-2}~\text{rad/s}\) clockwise
4.
\(2\times10^{-2}~\text{rad/s}\) clockwise
47. A narrow beam of light emerges from a source
\(S,\) gets reflected at
\(O\) from a plane mirror
\(MN,\) and forms a spot
\((P)\) on a wall, parallel to
\(MN.\) The distance between
\(S\) and the mirror is
\(40~\text{cm},\) and between the mirror and the wall is
\(60~\text{cm}.\) The mirror
\((MN)\) and the source
\((S)\) can rotate about axes perpendicular to the plane of the diagram. The angle of incidence of the ray
\(SO,\) on the mirror, is
\(45^\circ\) initially.

The mirror is fixed, but the source ray
\(SO\) rotates anticlockwise with an angular speed
\(10^{-2}~\text{rad/s}\) about
\(S.\) The linear speed of point
\(O\) on the mirror, is:
1.
\(4~\text{mm/s}\)
2.
\(8~\text{mm/s}\)
3.
\(4\sqrt2~\text{mm/s}\)
4.
\(8\sqrt2~\text{mm/s}\)
48. A narrow beam of light emerges from a source
\(S,\) gets reflected at
\(O\) from a plane mirror
\(MN,\) and forms a spot
\((P)\) on a wall, parallel to
\(MN.\) The distance between
\(S\) and the mirror is
\(40~\text{cm},\) and between the mirror and the wall is
\(60~\text{cm}.\) The mirror
\((MN)\) and the source
\((S)\) can rotate about axes perpendicular to the plane of the diagram. The angle of incidence of the ray
\(SO,\) on the mirror, is
\(45^\circ\) initially.

The mirror is fixed, but the source ray
\(SO\) rotates anticlockwise, with an angular speed
\(10^{-2}~\text{rad/s}\) about
\(S.\) The speed of the spot
\(P,\) on the wall, is:
1.
\(8~\text{mm/s}\)
2.
\(16~\text{mm/s}\)
3.
\(20~\text{mm/s}\)
4.
\(28~\text{mm/s}\)
49. A narrow beam of light emerges from a source
\(S,\) gets reflected at
\(O\) from a plane mirror
\(MN,\) and forms a spot
\((P)\) on a wall, parallel to
\(MN.\) The distance between
\(S\) and the mirror is
\(40~\text{cm},\) and between the mirror and the wall is
\(60~\text{cm}.\) The mirror
\((MN)\) and the source
\((S)\) can rotate about axes perpendicular to the plane of the diagram. The angle of incidence of the ray
\(SO,\) on the mirror, is
\(45^\circ\) initially.

The source ray is fixed, but the mirror
\(MN\) rotates clockwise about
\(O\) with an angular speed of
\(10^{-2}~\text{rad/s}.\) The speed of the spot, on the wall, is:
1.
\(8~\text{mm/s}\)
2.
\(12~\text{mm/s}\)
3.
\(16~\text{mm/s}\)
4.
\(24~\text{mm/s}\)
50. A narrow beam of light emerges from a source
\(S,\) gets reflected at
\(O\) from a plane mirror
\(MN,\) and forms a spot
\((P)\) on a wall, parallel to
\(MN.\) The distance between
\(S\) and the mirror is
\(40~\text{cm},\) and between the mirror and the wall is
\(60~\text{cm}.\) The mirror
\((MN)\) and the source
\((S)\) can rotate about axes perpendicular to the plane of the diagram. The angle of incidence of the ray
\(SO,\) on the mirror, is
\(45^\circ\) initially.

The source ray
\(SO\) rotates anticlockwise (about
\(S\)) with a speed of
\(10^{-2}~\text{rad/s},\) but the mirror
\(MN\) rotates clockwise about
\(O\) with an angular speed of
\(10^{-2}~\text{rad/s}.\) The angular speed of the reflected ray
\(OP\) is:
1. zero
2.
\(2\times10^{-2}~\text{rad/s}\)
3.
\(3\times10^{-2}~\text{rad/s}\)
4.
\(4\times10^{-2}~\text{rad/s}\)
*If above link doesn't work, please go to test link from where you got the pdf and fill OMR from there
CLICK HERE to get FREE ACCESS for 2 days of ANY NEETprep course