Physics - Section A
1. Two positive charges, each of magnitude
\(q,\) are placed at coordinates
\((a,0)\) and
\((-a,0),\) respectively. A negative charge
\(-q\) is positioned at the origin
\((0,0).\) If the negative charge is displaced by a small distance
\(y\) along the positive
\(y\)-axis
\((y\ll a),\) what will be the net electrostatic force acting on the negative charge after its displacement?
1.
\( \dfrac{q^{2} y}{4 \pi \varepsilon_{0} a^{3}}(-\hat{j})\)
2.
\( \dfrac{q^{2} y}{2 \pi \varepsilon_{0} a^{3}}(-\hat{j})\)
3.
\( \dfrac{q^{2} y}{2 \pi \varepsilon_{0} a^{2}}(-\hat{j})\)
4.
\( \dfrac{q^{2} y}{4 \pi \varepsilon_{0} a^{2}}(-\hat{j})\)
2. An electric field is given by: \(\vec{E}(x,~y)=4 x \hat{\imath}-3 y \hat{\jmath}\); the field being measured in \(\text{'V/m'}\) and the distances in \(\text{'m'}.\) The variation of the potential along the direction \((\hat i - \hat j)\) at the point \((2, 2)\) is given by:
1. \(-14 ~\text{V/m}\)
2. \(14 ~\text{V/m}\)
3. -\(7 \sqrt 2~\text{V/m}\)
4. \(7 \sqrt 2~\text{V/m}\)
3. A point charge \(q\) is placed on the \(x\)-axis at \(x=a;\) an identical charge is placed on the \(y\)-axis at \(y=a.\) At the origin is placed a charge \((-2q).\) The dipole moment of the charge distribution is:
1. \(2qa\)
2. \(\sqrt2qa\)
3. \(\dfrac{qa}{2}\)
4. \(\dfrac{qa}{\sqrt2}\)
4. Given below are two statements:
| Statement I: |
If there is no net charge inside a Gaussian surface, the net flux through the Gaussian surface is zero. |
| Statement II: |
If there is no net charge inside a Gaussian surface, the electric field at every point of the Gaussian surface is zero. |
| 1. |
Statement I is correct and Statement II is incorrect. |
| 2. |
Statement I is incorrect and Statement II is correct. |
| 3. |
Both Statement I and Statement II are correct. |
| 4. |
Both Statement I and Statement II are incorrect. |
5. Two capacitors, one of
\(3~\mu\text{F}\) and the other of
\(1~\mu\text{F}\) are charged to
\(2~\text{V},\) \(4~\text{V}\) and are connected to each other in either of the two ways: their like terminals together
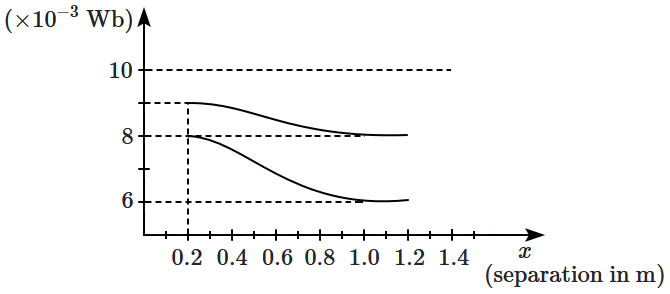
\((A)\) or unlike (i.e. oppositely charged) terminals together
\((B).\) The potential differences are
\(V_A, V_B\) in these cases. Then:
| 1. |
\(V_A= 2V_B\) |
2. |
\(V_A= 4V_B\) |
| 3. |
\(V_A=5V_B\) |
4. |
\(V_A = 6V_B\) |
6. The inter-plate capacitance of a pair of parallel metallic plates is given by the expression:
\(C={\large\frac{\varepsilon_0\times\text{area}}{\text{plate separation}}}\)
provided that the plate separation is very small compared to the dimensions of the area of the plate surface (not necessarily plane!). If the space between the plates is filled with a dielectric of dielectric constant
\(K,\) then the capacitance is
\(K\) times larger.
Two co-axial cylindrical metallic plates, of radii
\(R,R+d(d\ll R)\) and axial length
\(L,\) are placed as shown in the figure. The space between them is filled with a dielectric of relative permittivity
\(K.\) The capacitance of the system is (nearly)
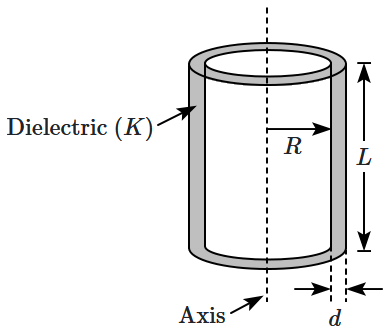
1.
\(K\varepsilon_0{\large\frac{\pi R^2}{d}}\)
2.
\(K\varepsilon_0{\large\frac{\pi RL}{d}}\)
3.
\(K\varepsilon_0{\large\frac{2\pi RL}{d}}\)
4.
\({\large\frac{K\varepsilon_0\pi R^2}{2d}}\)
7. Consider a uniformly charged hemispherical shell of radius
\(R,\) carrying a surface charge of density
\(\sigma.\) The potential at a point
\(P\) on the inner rim of the hemisphere is
\(V_P,\) while that at the center is
\(V_O,\) and the potential at the mid-point (
\(A\)) of
\(OP\) is
\(V_A.\) Then:
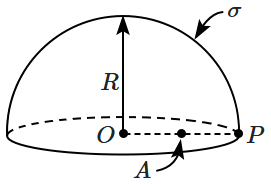
1.
\(V_O>V_A>V_P\)
2.
\(V_O<V_A<V_P\)
3.
\(V_A>V_O, V_A>V_P\)
4.
\(V_O=V_A=V_P\)
8. A pair of parallel plates of surface area
\(A\) are placed at a small distance
\(d\) from each other. If a dielectric of dielectric constant
\(K\) is inserted between the plates, the capacitance is:
| 1. |
\(\dfrac{\varepsilon_0A}{d}\) |
2. |
\(\dfrac{K\varepsilon_0A}{d}\) |
| 3. |
\(\dfrac{\varepsilon_0A}{K~d}\) |
4. |
\(\dfrac{(K+1)\varepsilon_0A}{d}\) |
9. A potential difference of
\(30~\text V\) is applied between the terminals
\(A,B\) of the circuit, shown in the figure.
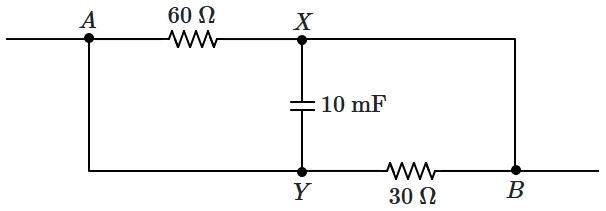
The energy stored in capacitance, in the steady state, is:
1. zero
2.
\(0.5~\text J\)
3.
\(2~\text J\)
4.
\(4.5~\text J\)
10. Two cylindrical capacitors are connected as shown in the figure:
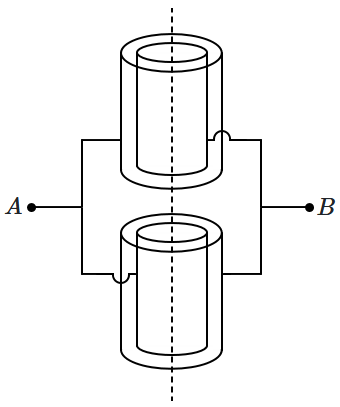
The two capacitors are identical, each having capacitance
\(C.\) The outer plate of the upper capacitor is connected to the inner plate of the lower capacitor and vice-versa. The net capacitance of the system, measured between
\(A~\&~B,\) is
1.
\(2C\)
2.
\({\dfrac{C}{2}}\)
3.
\(C\)
4.
\({\dfrac{5C}{4}}\)
11. A uniformly charged circular ring (of radius
\(R\)) has a total charge
\(Q;\) a second point charge
\(q\) is placed at the center of the ring. Consider a point
\(P\) on the axis of the ring, at a distance
\(x\) from its center. The radius of the ring subtends an angle
\(\theta\) at the point
\(P.\)
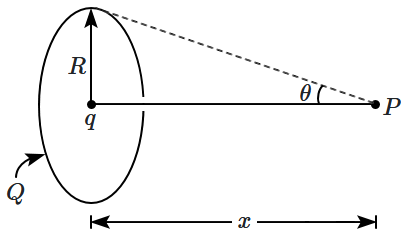
If the potential at
\(P\) due to all the charges is zero, then,
1.
\(\cos\theta=\Big|\dfrac qQ\Big|\)
2.
\(\cos^2\theta=\Big|\dfrac qQ\Big|\)
3.
\(\cos^3\theta=\Big|\dfrac qQ\Big|\)
4.
\(\cos^{\frac12}\theta=\Big|\dfrac qQ\Big|\)
12. A pair of concentric conducting spherical shells of radii
\(a,b\) are given charges
\(Q_1,Q_2\) respectively.
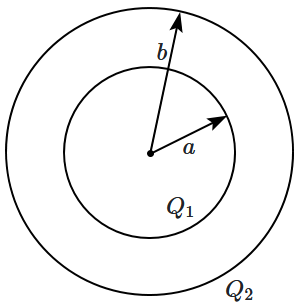
If
\(Q_1 = +Q\) and
\(Q_2 = -Q,\) and the potential difference between the spheres be
\(V,\) the ratio
\(\frac{Q}{V}\) is their capacitance.
The capacitance of this configuration is:
(
\(A_a=4\pi a^2,\) \(~A_b=4\pi b^2,\) separation
\(= d = b - a\))
1.
\(\varepsilon_0\dfrac{A_a}{d}\)
2.
\(\varepsilon_0\dfrac{(A_a+A_b)/2}{d}\)
3.
\(\varepsilon_0\dfrac{\sqrt{A_aA_b}}{d}\)
4.
\(\varepsilon_0\dfrac{A_b}{d}\)
13. The resistance of a newly invented device \((XY)\) is given by the relation:
\(R_{XY}= \begin{cases} (2000~\Omega/\text A)i, & \quad \text{when } i<50~\text{mA}\\ {\large\frac{5~\text V}{i}}, & \quad \text{when } i\geq50~\text{mA} \end{cases}\)
The current \(i\) cannot be negative. What is the maximum resistance of this device?
1. \(10~\Omega\)
2. \(100~\Omega\)
3. \(1000~\Omega\)
4. \(10^4~\Omega\)
14. A potential difference
\(V_{AB}\) is impressed across
\(AB\) and the potential difference across
\(CD\) \((V_{CD})\) is measured. Assume,
\(V_{AB}=300~\text{V}.\)
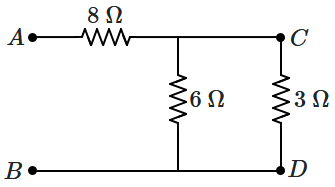
The current through the
\(8~\Omega\) resistance is:
1.
\(\dfrac{300}{17}~\text A\)
2.
\(\dfrac{300}{8.5}~\text A\)
3.
\(30~\text A\)
4.
\(\Big(\dfrac{300}{14}+\dfrac{300}{11}\Big)~\text A~~\)
15. Two identical resistances are once connected in parallel and then in series to a source of \(\text{V}~\text{volts}. \) The ratio of power consumed in parallel to that in series will be:
1. \(1:4\)
2. \(1:2\)
3. \(1:1\)
4. \(4:1\)
16. Two cells of unequal EMFs,
\(E_1\) and
\(E_2,\) and internal resistances
\(r_1\) and
\(r_2\) are joined as shown.
\(V_A\) and
\(V_B\) are the potentials at
\(A\) and
\(B\) respectively.
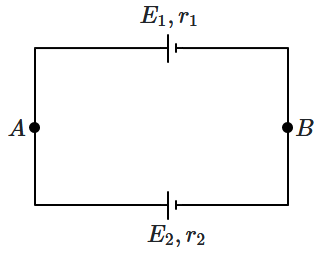
| (A) |
One cell will continuously supply energy to the other. |
| (B) |
The potential difference across both cells will be equal. |
| (C) |
The potential difference across one cell will be greater than its EMF. |
| (D) |
\(V_A-V_B={\large\frac{(E_1r_2+E_2r_2)}{(r_1+r_2)}}.\) |
Choose the correct option from the options given below:
1.
(A), (B), (C), and
(D)
2.
(A) and
(C) only
3.
(A) and
(D) only
4.
(B), (C) and
(D) only
17. Two batteries with emf \(12~\text{V}\) and \(13~\text{V}\) are connected in parallel across a load resistor of \(10~\Omega.\) The internal resistances of the two batteries are \(1~\Omega\) and \(2~\Omega\) respectively. The voltage across the load lies between:
1. \(11.6~\text{V}~\text{and}~11.7~\text{V}\)
2. \(11.5~\text{V}~\text{and}~11.6~\text{V}\)
3. \(11.4~\text{V}~\text{and}~11.5~\text{V}\)
4. \(11.7~\text{V}~\text{and}~11.8~\text{V}\)
18. In the circuit shown in the diagram, the resistance
\(r\) is unknown but fixed. The EMF
\(E\) can be varied and the current
\((i)\) passing through the ammeter
\({(A)}\) can be measured in magnitude only.
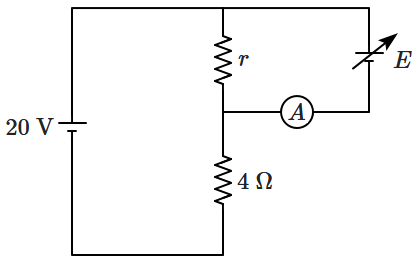
For a particular situation, it is observed that when
\(E = 4.8~\text V\) and when
\(E = 3.2~\text V,\) the ammeter gives the same reading in magnitude. Then, the value of the resistance
\(r\) is:
1.
\(1~\Omega\)
2.
\(2~\Omega\)
3.
\(1.6~\Omega\)
4.
\(4~\Omega\)
19. In the figure shown, each resistor has resistance
\(R.\)

Match
Column-I and
Column-II.
|
Column-I |
|
Column-II |
| (A) |
Equivalent resistance between \(a\) and \(b\) |
(P) |
\(\dfrac{R}{2}\) |
| (B) |
Equivalent resistance between \(a\) and \(c\) |
(Q) |
\(\dfrac{5R}{8}\) |
| (C) |
Equivalent resistance between \(b\) and \(d\) |
(R) |
\(R\) |
| 1. |
(A )→ (P), (B) → (Q), (C) → (R) |
| 2. |
(A) → (Q), (B) → (P), (C)→ (R) |
| 3. |
(A ) → (R), (B) → (P), (C) → (Q) |
| 4. |
(A ) → (R), (B) → (Q), (C) → (P) |
20. Choose the incorrect statement out of the following:
| 1. |
the relation \(V\text=IR\) applies to ohmic as well as non-ohmic conductors. |
| 2. |
the relation \(\vec{E} = \rho \vec{j}\) applies to all conducting devices, where \(\vec{E}\) is the electric field, \(\vec{j}\) is the current density, and \(\rho\) is resistivity. |
| 3. |
the resistance of an ohmic conductor is constant at a given temperature. |
| 4. |
the resistance of a non-ohmic conductor is a function of the applied voltage. |
21. A thin ring of \(10~\text{cm}\) radius carries a uniformly distributed charge. The ring rotates at a constant angular speed of \(40\pi ~\text{rad}~\text{s}^{-1}\) about its axis, perpendicular to its plane. If the magnetic field at its centre is \(3.8\times 10^{-9}~\text{T},\) then the charge carried by the ring is close to:
(\(\mu_0=4\pi\times 10^{-7}~\text{N/A}^2\))
1. \(7\times 10^{-6}~\text{C}\)
2. \(4\times 10^{-5}~\text{C}\)
3. \(2\times 10^{-6}~\text{C}\)
4. \(3\times 10^{-5}~\text{C}\)
22. A charge moving very fast in a circular path, e.g., an electron in an orbit around a nucleus, can be effectively considered to be equivalent to a current. Consider a charge \(q\) moving in a circular orbit of radius \(R,\) around another fixed charge of opposite sign: the angular speed of the moving charge being \(\omega.\) The magnetic field at the centre of the orbit, due to the motion of this charge \(q,\) is:
1. \(\dfrac{\mu_0q\omega}{4\pi R}\)
2. \(\dfrac{\mu_0q\omega}{2\pi R}\)
3. \(\dfrac{\mu_0q\omega}{2R}\)
4. \(\dfrac{\mu_0q(\omega R)}{2}\)
23. A long thin vertical cylindrical conducting pipe (radius
\(R\)) carries a uniform current
\(I\) flowing axially but distributed evenly along its circumference. The magnetic field on its axis, if a vertical, thin slice of a cylinder is removed – the slice forming a width
\(s~(s\ll R)\) of the circumference:
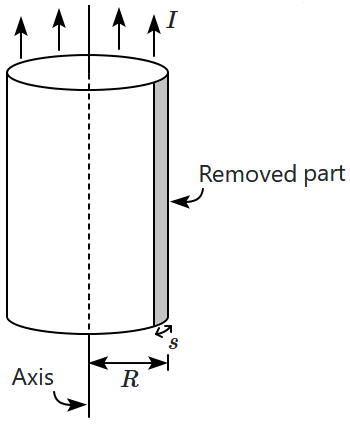
1.
\(\dfrac{\mu_0Is}{2\pi R}\)
2.
\(\dfrac{\mu_0Is}{2\pi R^2}\)
3.
\(\dfrac{\mu_0Is}{4\pi R}\)
4.
\(\dfrac{\mu_0Is}{4\pi^2 R^2}\)
24. A circular coil of wire carrying a current
\(I\) (ampere) is placed in a uniform magnetic field
\(B,\) which makes an angle of
\(60^{\circ}\) with the axis of the coil.
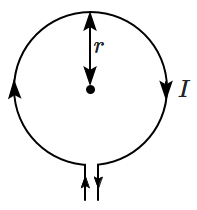
The torque on the coil, due to the magnetic field, is:
1.
\(I.4\pi r^2.B\)
2.
\(I.2\pi r^2.B\cos60^\circ\)
3.
\(I.\pi r^2.B\sin60^\circ\)
4. zero
25. An equilateral triangular current loop \(PQR\) carries a current \(I\) ampere. The length of each side is \(l\) meter. A uniform magnetic field of induction \(\vec B\) exists in a direction parallel to \(PQ.\) Then, the force on the side \(PQ\) is:
1. \(IlB\)
2. \(\dfrac{ IlB}{2}\)
3. \(\left(\dfrac{ IlB}{ 2}\right) \sqrt 3\)
4. zero
26. The resistance of a galvanometer is \(50~\Omega\) and the maximum current which can be passed through it is \(0.002~\text{A}\). What resistance must be connected to it in order to convert it into an ammeter of range \((0\text-0.5~\text{A})?\)
1. \(0.2~\Omega\)
2. \(0.002~\Omega\)
3. \(0.02~\Omega\)
4. \(0.5~\Omega\)
27. Magnetic fields at two points on the axis of a circular coil at a distance of \(0.05~\text m\) and \(0.2~\text m\) from the centre are in the ratio \(8:1.\) The radius of the coil is:
1. \(0.2~\mathrm{m}\)
2. \(0.1~\mathrm{m}\)
3. \(0.15~\mathrm{m}\)
4. \(1.0~\mathrm{m}\)
28. A square loop of wire carrying a current \(i_1\) and inscribed within a second circular loop of wire carrying a current \(i_2\) – both produce the same magnetic field at their common centre. The ratio of their magnetic moments i.e., \(m_1~\text{(square)}/m_2~\text{(circle)}=\)
1. \(2\)
2. \(1\)
3. \(\dfrac{1}{2}\)
4. \(\dfrac{16}{\pi^2}\)
29. The magnetic moment and moment of inertia of a magnetic needle as shown are, respectively,
\(1.0\times10^{-2}~\text{A m}^{2}~\text{and}~\frac{10^{-6}}{\pi^{2}}~\text{kg m}^{2}.\) If it completes
\(10\) oscillations in
\(10~\text s,\) the magnitude of the magnetic field is:

1.
\(0.4~\text T\)
2.
\(4~\text T\)
3.
\(0.4~\text{mT}\)
4.
\(4~\text{mT}\)
30. A regular array of identical vertical current-carrying wires, each passing through a horizontal table, is arranged as shown in the figure (with the direction of current flow indicated). Where are diamagnetic particles most likely to accumulate if they are scattered on the table?

| 1. |
Around regions such as \(A.\) |
| 2. |
Around regions such as \(B.\) |
| 3. |
In circular regions around individual wires such as \(C.\) |
| 4. |
Uniformly everywhere. |
31. Three identical bar magnets, each having a dipole moment \(M,\) are placed at the origin—oriented along the \(x\text-\)axis, the \(y\text-\)axis, and the \(z\text-\)axis respectively. The net magnetic moment of the dipoles has the magnitude:
1. \(3M\)
2. \(\sqrt2M\)
3. \(\sqrt3M\)
4. zero
32. A uniform magnetic field \(B\) exists in a cylindrical region; this field varies at a constant rate \(\frac{dB}{dt}.\) Consider a square loop \(PQRS\) centred in this region. The components of the induced \(E-\) field along the side of the square, at the points \(P\) and \(T\) (mid-point of \(PS\)) are in the ratio: \(\Big(i.e. \frac{E_P}{E_T}=\Big)\)
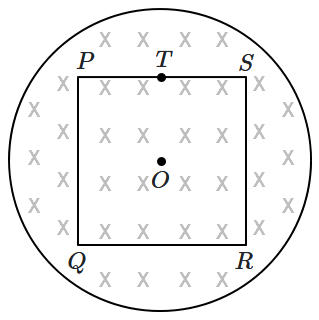
1. \(1\)
2. \(\sqrt2\)
3. \(\dfrac{1}{\sqrt2}\)
4. \(2\)
33. A rectangular conducting wire loop of dimension
\((PS\times PQ)~1~\text m\times2 ~\text m\) is pushed into a region having a constant magnetic field,
\(B=1.5~\text T,\) with a constant speed of
\(4~\text{m/s}\) (along
\(PQ\)). The boundary of the field makes an angle of
\(45^\circ\) with the side
\(PQ\) (figure). The resistance of the conducting loop is
\(200~\Omega.\)
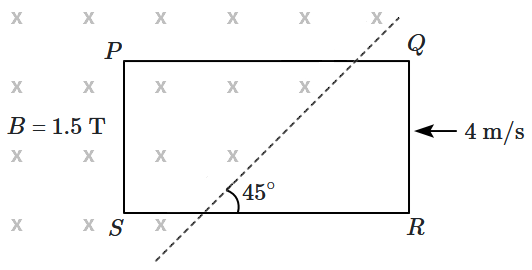
The current flowing through the loop has the magnitude,
1.
\(30~\text{mA}\)
2.
\(30\sqrt2~\text{mA}\)
3.
\(60~\text{mA}\)
4.
\(15\sqrt2~\text{mA}\)
34. Two identical
\(10~\text{mH}\) inductors are placed side-by-side, as shown in the figure. If the ends
\(Q,S\) are connected, the total inductance measured between
\(P,R\) is
\(18~\text{mH}.\) If the ends
\(Q,R\) are connected, the inductance between
\(P,S\) will be
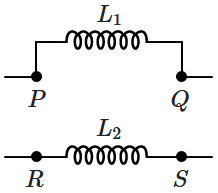
1.
\(20~\text{mH}\)
2.
\(18~\text{mH}\)
3.
\(16~\text{mH}\)
4.
\(22~\text{mH}\)
Physics - Section B
35. The RMS value of the current
\(I=a\sin\omega t \cos\omega t\) is:
1.
\(\dfrac{a}{\sqrt 2}\)
2.
\(\dfrac{a}{\sqrt 3}\)
3.
\(\dfrac{a}{2\sqrt 2}\)
4.
\(\dfrac{a}{2}\)
36. An alternating voltage of angular frequency
\(\omega\) is applied to the circuit shown in the figure.
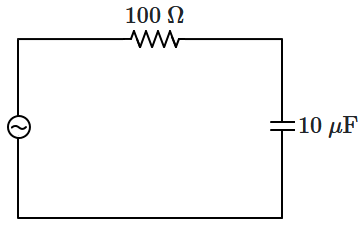
When the value of
\(\omega\) is adjusted so that the impedance of the capacitor and the resistor match, what is the net impedance in the circuit?
1. zero
2.
\(100~\Omega\)
3.
\(200~\Omega\)
4.
\(100\sqrt2~\Omega\)
37. A \(750~\text{Hz},\) \(20~\text V\) (RMS) source is connected to a resistance of \(100~\Omega,\) an inductance of \(0.1803~\text H\) and a capacitance of \(10~{\mu \text{F}},\) all in series. The time in which the resistance (heat capacity \(2~\text J/^\circ \text C\)) will get heated by \(10^\circ \text {C}\) (assuming no loss of heat to the surroundings) is close to:
1. \(365~\text{s}\)
2. \(418~\text{s}\)
3. \(245~\text{s}\)
4. \(348~\text{s}\)
38. A bird sitting on a single high-tension wire does not get electrocuted because:
| 1. |
the circuit is not complete. |
| 2. |
the bird's feet has an insulating covering. |
| 3. |
the capacitance of the bird is too small and the line frequency is too small. |
| 4. |
the resistance of the bird is too high. |
39. An alternating
\(\text{emf}= V_0\sin \omega t\) is applied between the two ends
\(A\) &
\(B\) of the circuit shown below. The current through
\(C\) has the same RMS value as that through
\(R.\) The RMS value of the current flowing out at
\(B\) is:

1.
\(\dfrac{V_0}{ \sqrt 2 R}\)
2.
\(\dfrac{V_0}{ R}\)
3.
\(\dfrac{ \sqrt 2 V_0}{R}\)
4. zero
40. A transformer consisting of \(300\) turns in the primary and \(150\) turns in the secondary gives output power of \(2.2~\text{kW}.\) If the current in the secondary coil is \(10~\text{A},\) then the input voltage and current in the primary coil are:
1. \(440~\text{V}~\text{and}~20~\text{A}\)
2. \(440~\text{V}~\text{and}~5~\text{A}\)
3. \(220~\text{V}~\text{and}~20~\text{A}\)
4. \(220~\text{V}~\text{and}~10~\text{A}\)
41. In a series
\(LCR\) circuit, the voltage drop across the resistance is
\(8~\text V,\) the capacitor is
\(12~\text V,\) and the inductor is
\(6~\text V.\) Then:
| 1. |
the voltage of the source will be leading the current in the circuit. |
| 2. |
the voltage drop across each element will be less than the applied voltage. |
| 3. |
the source voltage is \(10~\text V\). |
| 4. |
both (1) and (2) would happen. |
42. Given below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R):
| Assertion (A): |
Some snakes can ‘see’ a frog in pitch darkness. |
| Reason (R): |
The snake can sense the infrared radiation emanating from the frog. |
In the light of the above statements choose the correct answer from the options given below:
| 1. |
Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. |
(A) is True but (R) is False. |
| 4. |
Both (A) and (R) are False. |
43. Electromagnetic waves, given by, \(\overrightarrow E_1=(2\times10^{-3}~\text{V/m})\hat j\sin(\omega t-kx)\) and \(\overrightarrow E_2=(1.5\times10^{-3}~\text{V/m})\hat k\sin(\omega t-kx)\) are travelling through space. Here, \(\omega=6\pi\times10^{14}~\text{s}^{-1}\) and \(k=2\pi\times10^{6}~\text{m}^{-1}.\) The amplitude of the electric field oscillations equals:
1. \(3.5\times10^{-3}~\text{V/m}\)
2. \(0.5\times10^{-3}~\text{V/m}\)
3. \(2.5\times10^{-3}~\text{V/m}\)
4. \(\sqrt3\times10^{-3}~\text{V/m}\)
44. Select the correct option based on the statements given below:
| Statement I: |
For cooking in a microwave oven, food is always kept in metal containers. |
| Statement II: |
The energy of the microwave is easily transferred to the food in a metal container. |
| 1. |
Statement I is correct and Statement II is incorrect. |
| 2. |
Statement I is incorrect and Statement II is correct. |
| 3. |
Both Statement I and Statement II are correct. |
| 4. |
Both Statement I and Statement II are incorrect. |
45. Two inductors are placed with their axes parallel to each other and their initial separation is
\(x_0=0.2~\text m.\) They carry currents of
\(1~\text A\) &
\(2~\text A,\) both from left to right (see figure) – i.e., from
\(A\) to
\(B\) & from
\(C\) to
\(D.\)
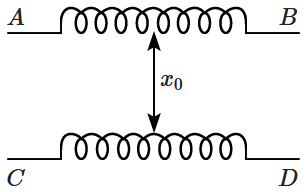
The flux linked through each of these is measured as a function of their separation and the graphs are shown.
The two inductors are moved far apart and joined in parallel. The net inductance will be (in
\(\text{mH}\))
1.
\(\dfrac{12}{7}\)
2.
\(\dfrac{12}{5}\)
3.
\(\dfrac{24}{7}\)
4.
\(\dfrac{24}{11}\)
46. Two inductors are placed with their axes parallel to each other and their initial separation is
\(x_0=0.2~\text m.\) They carry currents of
\(1~\text A\) &
\(2~\text A,\) both from left to right (see figure) – i.e., from
\(A\) to
\(B\) & from
\(C\) to
\(D.\)

The flux linked through each of these is measured as a function of their separation and the graphs are shown.

The two inductors are moved far apart and joined in series. The overall inductance will be (in
\(\text{mH}\))
1.
\(7\)
2.
\(11\)
3.
\(14\)
4.
\(10\)
47. Two inductors are placed with their axes parallel to each other and their initial separation is
\(x_0=0.2~\text m.\) They carry currents of
\(1~\text A\) &
\(2~\text A,\) both from left to right (see figure) – i.e., from
\(A\) to
\(B\) & from
\(C\) to
\(D.\)

The flux linked through each of these is measured as a function of their separation and the graphs are shown.

The end
\(B\) is connected to
\(C\) and the total inductance is measured between
\(A\) &
\(D,\) keeping the separation at
\(x_0=0.2~\text{m}.\) The value will be (in
\(\text{mH}\))
1.
\(12\)
2.
\(12.5\)
3.
\(13\)
4.
\(8\)
48. Two inductors are placed with their axes parallel to each other and their initial separation is
\(x_0=0.2~\text m.\) They carry currents of
\(1~\text A\) &
\(2~\text A,\) both from left to right (see figure) – i.e., from
\(A\) to
\(B\) & from
\(C\) to
\(D.\)

The flux linked through each of these is measured as a function of their separation and the graphs are shown.

The end
\(B\) is connected to
\(D\) and the total inductance is measured between
\(A\) &
\(C,\) keeping the separation at
\(x_0=0.2~\text{m}.\) The inductance is (in
\(\text{mH}\))
1.
\(12\)
2.
\(9\)
3.
\(8\)
4.
\(7.5\)
49. Two inductors are placed with their axes parallel to each other and their initial separation is
\(x_0=0.2~\text m.\) They carry currents of
\(1~\text A\) &
\(2~\text A,\) both from left to right (see figure) – i.e., from
\(A\) to
\(B\) & from
\(C\) to
\(D.\)

The flux linked through each of these is measured as a function of their separation and the graphs are shown.

The ends
\(A\) &
\(C\) are connected to a single terminal;
\(B\) &
\(D\) are connected to another terminal. The separation between the two inductors is kept at
\(x_0=0.2~\text m.\) The inductance, measured between these terminals, is (in
\(\text{mH}\))
1.
\(\dfrac{35}{12}\)
2.
\(\dfrac{15}{8}\)
3.
\(\dfrac{23}{8}\)
4.
\(\dfrac{23}{12}\)
50. Two inductors are placed with their axes parallel to each other and their initial separation is
\(x_0=0.2~\text m.\) They carry currents of
\(1~\text A\) &
\(2~\text A,\) both from left to right (see figure) – i.e., from
\(A\) to
\(B\) & from
\(C\) to
\(D.\)

The flux linked through each of these is measured as a function of their separation and the graphs are shown.

The ends
\(A\) &
\(D\) are connected to a single terminal;
\(B\) &
\(C\) are connected to another terminal.
The separation between the two inductors is kept at
\(x_0=0.2~\text m.\) The inductance
(in
\(\text{mH}\)), measured between these terminals, is
1.
\(\dfrac{35}{12}\)
2.
\(\dfrac{15}{8}\)
3.
\(\dfrac{23}{8}\)
4.
\(\dfrac{23}{12}\)
*If above link doesn't work, please go to test link from where you got the pdf and fill OMR from there
CLICK HERE to get FREE ACCESS for 2 days of ANY NEETprep course






























