Please be patient as the PDF generation may take upto a minute.

Four particles each having charge q are placed at the vertices of a square of side a. The value of the electric potential at the midpoint of one of the side will be
1.  0
2.  $\frac{1}{4\pi {ϵ}_0}\frac{2q}{a}(2+\frac{2}{\sqrt{5}})$
3.  $\frac{1}{4\pi {ϵ}_0}\frac{2q}{a}(2-\frac{2}{\sqrt{5}})$
4.  $\frac{1}{4\pi {ϵ}_0}\frac{2q}{a}(1+\frac{1}{\sqrt{5}})$

The electric potential at the surface of a charged solid sphere of insulator is 20V. The value of electric potential at its centre will be
1.  30V
2.  20V
3.  40V
4.  Zero

A hollow charged metal spherical shell has radius R. If the potential difference between its surface and a point at a distance 3R from the center is V, then the value of electric field intensity at a point at distance 4R from the center is
1.  $\frac{3\mathrm{V}}{19\mathrm{R}}$
2.  $\frac{\mathrm{V}}{6\mathrm{R}}$
3.  $\frac{3\mathrm{V}}{32\mathrm{R}}$
4.  $\frac{3\mathrm{V}}{16\mathrm{R}}$

The figure shows some of the equipotential surfaces. Magnitude and direction of the electric field is given by
           
1.  200 V/m, making an angle ${120}^0$ with the x-axis
2. 100 V/m, pointing towards the negative x-axis
3. 200 V/m, making an angle $-{60}^0$ with the x-axis
4. 100 V/m, making an angle ${30}^0$ with the x-axis

$\mathrm{The} \mathrm{electric} \mathrm{potential} \mathrm{at} \mathrm{a} \mathrm{point} \mathrm{at} \mathrm{distance} \sqrt{3}\mathrm{R} \mathrm{from} \mathrm{the} \mathrm{centre} \mathrm{of} \mathrm{disc}$
$\mathrm{of} \mathrm{radius} \mathrm{R} \mathrm{lying} \mathrm{in} \mathrm{the} \mathrm{axis} \mathrm{of} \mathrm{the} \mathrm{disc} \mathrm{whose} \mathrm{surface} \mathrm{charge} \mathrm{density} \mathrm{is} \mathrm{\sigma }$
$\mathrm{will} \mathrm{be} \mathrm{given} \mathrm{by}:$
$1. \frac{\sigma }{2{\epsilon }_0}\left[2-\sqrt{3}\right]R 2. \frac{\sigma }{2{\epsilon }_0}\left[2+\sqrt{3}\right]R$
$3.\frac{\sigma }{2{\epsilon }_0}\left[\sqrt{3}-\sqrt{2}\right]R 4. \frac{\sigma }{2{\epsilon }_0}\left[\sqrt{3}+\sqrt{2}\right]R$

Two small spheres each carrying a charge q are placed r meter apart. If one of the spheres is taken around the other one in a circular path of radius r, the work done will be equal to 
(1) Force between them × r
(2) Force between them × 2πr
(3) Force between them / 2πr
(4) Zero

The electric potential V at any point O (x, y, z all in metres) in space is given by $V=4x^{2}volt$. The electric field at the point $(1m,0,2m)$ in volt/metre is -
(1) 8 along negative x-axis
(2) 8 along positive x-axis
(3) 16 along negative x-axis
(4) 16 along positive z-axis

In the electric field of a point charge q, a certain charge is carried from point A to B, C, D and E. Then the work done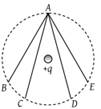


(1) Is least along the path AB
(2) Is least along the path AD
(3) Is zero along all the paths AB, AC, AD and AE
(4) Is least along AE

Two equal charges q are placed at a distance of 2a and a third charge –2q is placed at the midpoint. The potential energy of the system is -
(1) $\frac{q^2}{8\pi {\epsilon }_{0}a}$
(2) $\frac{6q^2}{8\pi {\epsilon }_{0}a}$
(3) $-\frac{7q^2}{8\pi {\epsilon }_{0}a}$
(4) $\frac{9q^2}{8\pi {\epsilon }_{0}a}$

How much kinetic energy will be gained by an $\alpha$– particle in going from a point at 70 V to another point at 50 V ?
(1) $40eV$
(2) $40keV$
(3) $40MeV$
(4) $0eV$

Three charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown. The net electrostatic energy of the configuration is zero if Q is equal to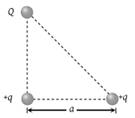


(1) $\frac{-q}{1+\sqrt{2}}$
(2) $\frac{-2q}{2+\sqrt{2}}$
(3) –2q
(4) +q

Figure shows three points A, B and C in a region of uniform electric field $\overrightarrow{E}$. The line AB is perpendicular and BC is parallel to the field lines. Then which of the following holds good. Where $V_A,V_B$ and V_C represent the electric potential at points A, B and C respectively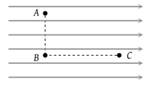


(1) $V_A=V_B=V_C$
(2) $V_A=V_B>V_C$
(3) $V_A=V_B<V_C$
(4) $V_A>V_B=V_C$

Two charges q₁ and q₂ are placed 30 cm apart, as shown in the figure. A third charge q₃ is moved along the arc of a circle of radius 40 cm from C to D. The change in the potential energy of the system is $\frac{q_3}{4\pi {\epsilon }_0}k$, where k is:
     

Two thin wire rings each having a radius R are placed at a distance d apart with their axes coinciding. The charges on the two rings are +q and –q. The potential difference between the centres of the two rings is -
(1) Zero
(2) $\frac{Q}{4\pi {\epsilon }_0}\left[\frac{{\displaystyle 1}}{{\displaystyle R}}-\frac{{\displaystyle 1}}{{\displaystyle \sqrt{R^2+d^2}}}\right]$
(3) $QR/4\pi {\epsilon }_0{d}^2$
(4) $\frac{Q}{2\pi {\epsilon }_0}\left[\frac{{\displaystyle 1}}{{\displaystyle R}}-\frac{{\displaystyle 1}}{{\displaystyle \sqrt{R^2+d^2}}}\right]$

64 drops each having the capacity C and potential V are combined to form a big drop. If the charge on the small drop is q, then the charge on the big drop will be 
(1) 2q
(2) 4q
(3) 16q
(4) 64q

Three concentric spherical shells have radii a, b and c (a<b<c) and have surface charge densities $\mathrm{\sigma }, -\mathrm{\sigma }$ and $\mathrm{\sigma }$ respectively. If ${\mathrm{V}}_{\mathrm{A}}, {\mathrm{V}}_{\mathrm{B}}$ and ${\mathrm{V}}_{\mathrm{C}}$ denote the potential of the three shells, if c=a+b, we have
(1) ${\mathrm{V}}_{\mathrm{C}}={\mathrm{V}}_{\mathrm{A}}\ne {\mathrm{V}}_{\mathrm{B}}$                                       
(2) ${\mathrm{V}}_{\mathrm{C}}={\mathrm{V}}_B\ne {\mathrm{V}}_{\mathrm{A}}$
(3) ${\mathrm{V}}_{\mathrm{C}}\ne {\mathrm{V}}_B\ne {\mathrm{V}}_A$                                       
(4) ${\mathrm{V}}_{\mathrm{C}}={\mathrm{V}}_B={\mathrm{V}}_A$

A solid conducting sphere having a charge Q is surrounded by an uncharged concentric conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a charge of –3Q, the new potential difference between the same two surfaces is 
(1) V
(2) 2V
(3) 4V
(4) –2V

In the figure, two conducting concentric spherical shells are shown.
                           
If the electric potential at the centre is 20V and the electric potential at the surface of outer shell is 5V, then the potential at the surface of inner shell is –
1.  5V                   
2.  15V 
3.  20V                 
3.  cannot be determined as radii are not given

Figure shows a ball having a charge \(q\) fixed at a point $\mathrm{A}$. Two identical balls having charges \(+q\) and \(–q\) and mass \(‘m’\) each are attached to the ends of a light rod of length $\mathrm{}$\(2 a\)\(2a\). The rod is free to rotate about a fixed axis perpendicular to the plane of the paper and passing through the mid-point of the rod. The system is released from the situation as shown in the figure. The angular velocity of the rod when the rod becomes horizontal will be: